|
Квантовые эффекты заторможенного вращения орто-пара-диводородов H2, D2, T2 при низкотемпературной адсорбции
В.С. Парбузин, Е.Б. Иванов
МГУ им. М.В.Ломоносова, Химический факультет
Макроскопические
проявления квантовых свойств вещества в адсорбированном состоянии связаны с
квантованием различных степеней свободы, дифракционными свойствами материи и
принадлежностью к различным статистикам – Бозе-Эйнштейна или Ферми-Дирака. Все
эти эффекты в полной мере проявляются у адсорбированных изотопов гелия Не-3 и
Не-4 и ,частично, у членов диводородного семейства, к которым относятся
гомоядерные молекулы орто-пара-протий, орто-пара-дейтерий, орто-пара-тритий и гетероядерные
HD, HT, DT. Избирательная адсорбция
диводородов есть проявление квантовых законов на макроскопическом уровне.
Решающую роль в селективной адсорбции спин-изомеров водорода играют различия
квантованных вращательных состояний двухатомных молекул диводородов в газе и на
поверхности сорбента, в результате чего спин-изомеры с нечетными вращательными
квантовыми числами (J=1,3,5,…) преимущественно накапливаются в
адсорбционной, а с четными (J =
0,2,4…) - в газовой фазе.
В докладе в
приближении жесткого ротатора рассматриваются квантовые модели заторможенного
вращения диводородов в трех типах адсорбционных полей:
1) на однородной
поверхности, где V = 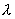 cos2 cos2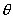
2) на
неоднородной поверхности, где V = 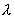 cos2 cos2 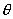 + + 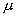 (1- cos2 (1- cos2 ) )
3) внутри
октаэдрической ячейки, где потенциал имеет вид
V = - 1/8 Vo[3 – 30cos2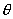 + 35cos4 + 35cos4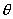 + 5sin4 + 5sin4 ∙cos4 ∙cos4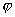 ] ]
Здесь V –
потенциал, 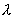 , ,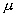 , Vo - вращательные барьеры; , Vo - вращательные барьеры; 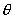 , , 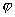 - полярные углы. С помощью компьютерного решения
соответствующих уравнений Шредингера получены уровни энергии и рассчитаны
теоретические температурные зависимости коэффициентов разделения
орто-пара-изомеров H2 и D2, которые сопоставлены с
собственными и литературными экспериментальными данными для силикагеля, оксида
алюминия и цеолитов. Обсуждаются адекватность и прогностический потенциал трех
моделей в приложении к реальным сорбентам. Сформулированы возможности
экспериментальной проверки предсказаний теории для разделения орто-пара-трития,
для которого такие измерения до сих пор отсутствуют. - полярные углы. С помощью компьютерного решения
соответствующих уравнений Шредингера получены уровни энергии и рассчитаны
теоретические температурные зависимости коэффициентов разделения
орто-пара-изомеров H2 и D2, которые сопоставлены с
собственными и литературными экспериментальными данными для силикагеля, оксида
алюминия и цеолитов. Обсуждаются адекватность и прогностический потенциал трех
моделей в приложении к реальным сорбентам. Сформулированы возможности
экспериментальной проверки предсказаний теории для разделения орто-пара-трития,
для которого такие измерения до сих пор отсутствуют.
|
