1.1. Наибольшая длина волны соответствует наименьшей разности энергий, т.е. переходу n = 2 n = 3. Для He⁺ (заряд ядра +2)

, = 164.11 нм.

1.2.

E = –hcR_H = –13.6 эВ.

1.3.Энергия в данной модели прямо пропорциональна массе, а радиус обратно пропорционален массе:

энергия основного состояния мюония = –207 13.6 = –2.82 кЭв;

радиус первой боровской орбиты мюония = 0.53 / 207 = 2.6 10^–3 Е.

1.4 Вероятность = [ (a₀)] ² 4 a₀² 0.001 a₀ = 0.004 e^–2 = 5.41 10^–4.

1.5 Мелкая кривая – первый канал (диссоциация на атомы), глубокая кривая – второй канал (диссоциация на ионы).

1.6 Первый канал: D_e = 2 (–13.6) – (–31.9) = 4.7 эВ.
Второй канал: D_e = (–14.3) – (–31.9) = 17.6 эВ.

1.7.Сродство к электрону: E(H) – E(H^–) = –13.6 – (–14.3) = 0.7 эВ.

1.8 Энергия каждого электрона в H- равна 13.6 Z_eff². Для вылета обоих электронов требуется 14.3 эВ:
2 13.6 Z_eff² = 14.3, откуда Z_eff = 0.73.

33 МХО Задача 2

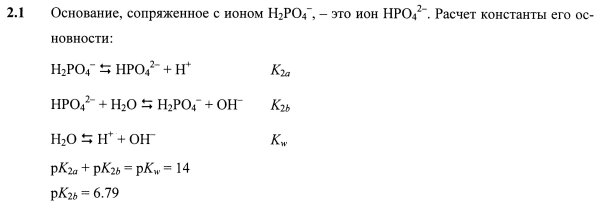
2.2.

2.3 Обозначим PO₄ = X и мольные доли фосфоросодержащих частиц: f₀ = [H₃X] / C, f₁ = [H₂X^–] / C, f₂ = [HX^2–] / C, f₃ = [X^3–] / C, где C = 1.00 10^–3 M – исходная концентрация фосфорной кислоты: f₀ + f₁ + f₂ + f₃ = 1.

K_1a = [H₂X^–] [H⁺] / [H₃X] = [H⁺] f₁ / f₀.

K_2a = [HX^2–] [H⁺] / [H₂X^–] = [H⁺] f₂ / f₁.

K_3a = [X^3–] [H⁺] / [HX^2–] = [H⁺] f₃ / f₂.

Из этих уравнений можно выразить мольные доли:

f₀ = [H⁺]³ / D, f₁ = [H⁺]² K_1a / D, f₂ = [H⁺] K_1a K_2a / D, f₃ = K_1a K_2a K_3a / D, где

D = K_1a K_2a K_3a + K_1a K_2a [H⁺] + K_1a [H⁺]² + [H⁺]³.

Из значений pK и pH следует: K_1a = 7.59 10^–3, K_2a = 6.17 10^–8, K_3a = 4.79 10^–13, [H⁺] = 10^–7. Отсюда мольные доли фосфоросодержащих частиц при pH = 7:

H₃PO₄: f₀ = 8.10 10^–6,

H₂PO₄^–: f₁ = 0.618,

HPO₄^2–: f₂ = 0.382,

PO₄^3–: f₃ = 1.83 10^–6.

2.4 Пусть S – молярная концентрация фосфата цинка в воде, тогда [Zn²⁺] = 3S, общая концентрация фосфоросодержащих частиц – 2S, а [PO₄^3–] = f₃ 2S (f₃ = 1.83 10^–6).

ПР = 9.1 10^–33 = [Zn²⁺]³ [PO₄^3–]² = (3S)³ (f₃ 2S)², откуда S = 3.0 10^–5.

[Zn²⁺] = 9.0 10^–5,

[PO₄^3–] = 1.1 10^–10.

3.1.При расширении энтропия газа увеличивается, а энтропия окружающей среды уменьшается, т.к. газ при расширении забирает теплоту из окружения. Правильный ответ (в).

3.2 S_сис = nR ln(V₂/V₁) = 27.4 Дж/К.

3.3 Q = P V = 100 20 = 2000 Дж. S_окр = –Q / T = –2000 / 288 = –6.94 Дж/К.

3.4  S_всел =  S_сис +  S_окр = 20.5 Дж/К. Положительное изменение энтропии находится в согласии со Вторым законом термодинамики.

3.5 Правильный ответ – (б).

3.6 Правильный ответ – (а).

3.7.Следствие из уравнения Клапейрона-Клаузиуса: ln(P₂/P₁) = H_субл / R (1/T₁ – 1/T₂), P₂ = 5.18 бар, P₁ = 1.01 бар, T₂ = 273.15 – 56.6, T₁ = 273.15 – 78.5. H_субл = 26.1 кДж/моль.

3.8 CO_2(г) + С_(тв) = 2CO_(г).

_rH^o = 2 (- 110.53) - (- 393.51) = 172.45 кДж;

_rS^o = 2 (197.66) - 213.79 - 5.74 = 175.79 Дж/К;

_rG^o = _rH^o - T _rS^o = 120.06 кДж;

_rG^o > 0. K_P = exp(- _rG^o/RT) < 1.

3.9 K_P = 1, _rG^o = 0.

T = _rH^o / _rS^o = 980 К.

3.10. P(CO) = x, P(CO₂) = 5.0 - x.

K_P = 10.0 = x² / (5.0 - x).

x = P(CO) = 3.7 бар.

4.1.Пусть N₀ – исходное число атомов тория-232, N – их число в настоящий момент, тогда образовалось N₀ – N атомов свинца-208.

N = N₀ exp(–0.693t / t_1/2).

(N₀ – N) / N = 0.104

exp(0.693t / 1.41 10¹⁰) = 1.104

t = 2.01 10⁹ лет.

4.2 ²⁰⁶Pb/²³⁸U = exp(–0.693t / t_1/2) – 1 = exp(0.693 2.01 10⁹ / 4.47 10⁹) – 1 = 0.366.

4.3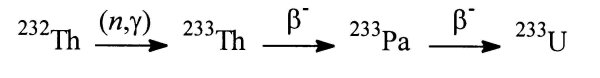

4.4 1) 14.6 мин – период полураспада ¹⁰¹Mo, поэтому число атомов ¹⁰¹Mo равно:
N₁ = N₀ / 2 = 25000.

2) В системе последовательных реакций первого порядка число атомов промежуточного вещества ¹⁰¹Tc дается выражением:,

3) Число атомов ¹⁰¹Ru при t = 14.6 мин:

N₃ = N₀ – N₁ – N₂ = 7900.