2.2.2. Смешение газов
Пусть в отдельных термостатированных сосудах под одинаковым давлением p
находятся газы А и В, взятые в количествах  и и молей. При соединении этих сосудов
произойдет самопроизвольное смешение газов вплоть до установления однородного
состава газовой смеси по всему объему системы. Будем предполагать, что исходные
газы и их смеси подчиняются уравнениям состояния идеальных газов. Тогда при
сохранении постоянного общего давления газов p парциальные
давления газов в образовавшейся смеси будут равны молей. При соединении этих сосудов
произойдет самопроизвольное смешение газов вплоть до установления однородного
состава газовой смеси по всему объему системы. Будем предполагать, что исходные
газы и их смеси подчиняются уравнениям состояния идеальных газов. Тогда при
сохранении постоянного общего давления газов p парциальные
давления газов в образовавшейся смеси будут равны
 . (2.8) . (2.8)
При смешении идеальных газов тепловые эффекты отсутствуют, поэтому
теплообмена между газами и термостатом не происходит, и изменение энтропии
системы будет полностью определяться необратимостью процессов внутри системы.
Чтобы найти искомое изменение энтропии, необходимо противопоставить
описанному самопроизвольному процессу мысленный равновесный переход между теми
же начальным и конечным состояниями системы.
Для равновесного смешения газов воспользуемся специальным гипотетическим
устройством, по аналогии с термостатомназываемым хемостатом. Это
устройство состоит из термостатируемого цилиндра, снабженного перемещающимся
без трения поршнем; в основании цилиндра находится избирательно проницаемая
только для данного индивидуального химического вещества мембрана; последняя
отделяет индивидуальное вещество, загруженное в хемостат, от изучаемой смеси
веществ, находящейся в другом сосуде. В отличие от термостата, предназначенного
для поддержания заданной температуры погруженного в него тела, либо для
нагревания или охлаждения последнего в равновесном режиме, с помощью хемостата
обеспечивают поддержание определенного значения химического потенциала данного
индивидуального вещества в исследуемой смеси веществ, а также равновесный
подвод и отвод вещества из смеси. Химический потенциал  i-гохимического
компонента в хемостате однозначно определяется температурой T и
давлением, создаваемым на поршне. Изменяя давление на поршне, можно изменять
направление перехода данного компонента через селективную мембрану: если i-гохимического
компонента в хемостате однозначно определяется температурой T и
давлением, создаваемым на поршне. Изменяя давление на поршне, можно изменять
направление перехода данного компонента через селективную мембрану: если  – химический
потенциал компонента в исследуемой смеси, то при – химический
потенциал компонента в исследуемой смеси, то при  вещество будет подводиться в
смесь, при вещество будет подводиться в
смесь, при  –
выводиться из смеси, и при –
выводиться из смеси, и при  между хемостатом и смесью поддерживается химическое
равновесие. Квазиравновесному изменению состава смеси соответствует
диффузионный перенос вещества через мембрану под действием весьма малой
разности значений химического потенциала по обе стороны мембраны. между хемостатом и смесью поддерживается химическое
равновесие. Квазиравновесному изменению состава смеси соответствует
диффузионный перенос вещества через мембрану под действием весьма малой
разности значений химического потенциала по обе стороны мембраны.
Химический потенциал идеального газа, независимо от того, находится ли этот
газ в индивидуальном состоянии или же в смеси с другими идеальными газами,
выражается простым соотношением  , где pi
есть либо давление чистого газа, либо его парциальное давление в смеси. Поэтому
при переносе идеального газа через полупроницаемую мембрану равновесие между
смесью и хемостатом характеризуется равенством давления в хемостате и
парциального давления газа в смеси. , где pi
есть либо давление чистого газа, либо его парциальное давление в смеси. Поэтому
при переносе идеального газа через полупроницаемую мембрану равновесие между
смесью и хемостатом характеризуется равенством давления в хемостате и
парциального давления газа в смеси.

Рис. 2.3. Равновесное смешение
двух газов с помощью хемостатов: a – начальное состояние системы; б
– состояние системы после изотермического расширения газов; в – конечное
состояние после смешения газов через мембраны; 1 – хемостаты индивидуальных
газов A и B; 2 – полупроницаемые мембраны; 3 –
сосуд для равновесного смешения газов.
Равновесное смешение идеальных газов A и B проведем в
термостатируемой системе, состоящей из двух хемостатов индивидуальных
компонентов A и B, соединенных с третьим сосудом – сборником
образующейся смеси, снабженным, так же как и хемостаты, подвижным поршнем (рис.
2.3).
Пусть в начальный момент в хемостатах содержится соответственно  молей компонента
A и молей компонента
A и  молей
компонента B под одинаковым давлением p; поршень в
сборнике смеси находится в нулевой позиции (объем газа под поршнем равен нулю).
Процесс смешения проводим в два этапа. На первом этапе совершаем обратимое
изотермическое расширение газов A и B; при этом давление A
снижаем от p до заданного давления молей
компонента B под одинаковым давлением p; поршень в
сборнике смеси находится в нулевой позиции (объем газа под поршнем равен нулю).
Процесс смешения проводим в два этапа. На первом этапе совершаем обратимое
изотермическое расширение газов A и B; при этом давление A
снижаем от p до заданного давления  и давление B соответственно
от p до и давление B соответственно
от p до 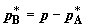 . Объемы, занимаемые газами в первом и во втором хемостатах,
изменятся соответственно от . Объемы, занимаемые газами в первом и во втором хемостатах,
изменятся соответственно от  до до  и от и от  до до  . Работа, совершенная расширяющимся газом в первом хемостате,
равна . Работа, совершенная расширяющимся газом в первом хемостате,
равна  ; во
втором ; во
втором  .
Таким образом, на первом этапе в нашем гипотетическом устройстве производится
суммарная работа .
Таким образом, на первом этапе в нашем гипотетическом устройстве производится
суммарная работа  . Так как при изотермическом расширении идеального газа его
внутренняя энергия не изменяется, указанная работа осуществляется за счет
эквивалентного подвода теплоты из термостата . Так как при изотермическом расширении идеального газа его
внутренняя энергия не изменяется, указанная работа осуществляется за счет
эквивалентного подвода теплоты из термостата  . Отсюда обратимое изменение энтропии в
системе будет равно . Отсюда обратимое изменение энтропии в
системе будет равно
 . (2.9) . (2.9)
На втором этапе процесса (собственно смешении) производим перепускание газов
из хемостатов через селективные мембраны в сборник смеси путем
синхронизированного движения трех поршней. При этом на каждом из поршней
поддерживается постоянное давление, соответственно,  и и  в хемостатах и в хемостатах и  в сборнике, что
обеспечивает равновесный переход газов через мембраны (точнее говоря, в
сборнике создается давление, чуть меньшее p, сохраняя отличную
от нуля движущую силу диффузии через мембраны). Обратимость процесса смешения в
данном случае обеспечивается возможностью синхронного изменения направления
движения всех трех поршней, что приводило бы к обратному разделению смеси на
индивидуальные компоненты. После завершения операции смесь, очевидно, займет в
сборнике объем в сборнике, что
обеспечивает равновесный переход газов через мембраны (точнее говоря, в
сборнике создается давление, чуть меньшее p, сохраняя отличную
от нуля движущую силу диффузии через мембраны). Обратимость процесса смешения в
данном случае обеспечивается возможностью синхронного изменения направления
движения всех трех поршней, что приводило бы к обратному разделению смеси на
индивидуальные компоненты. После завершения операции смесь, очевидно, займет в
сборнике объем  . .
Так как в случае идеальных газов смешение не сопровождается каким-либо
тепловым эффектом, теплообмен нашего устройства с термостатом на втором этапе
операции отсутствует,  . Следовательно, изменение энтропии системы на этом этапе не
происходит, . Следовательно, изменение энтропии системы на этом этапе не
происходит,  . .
Полезно убедиться путем прямого подсчета, что работа газов на втором этапе
равна нулю. Действительно, на перемещение поршней в хемостатах расходуется
работа  , в
то же время в сборнике газами производится та же самая по величине работа , в
то же время в сборнике газами производится та же самая по величине работа  . Отсюда . Отсюда  . .
Итак, суммарный прирост энтропии при смешении газов определяется выражением
(2.9),  .
Если при равновесном варианте смешения этот прирост связан с обратным подводом
теплоты и производством эквивалентного количества работы .
Если при равновесном варианте смешения этот прирост связан с обратным подводом
теплоты и производством эквивалентного количества работы  , то при прямом
(необратимом) смешении газов этот же прирост энтропии происходит за счет ее
генерации внутри системы; никакой работы система при этом не совершает. , то при прямом
(необратимом) смешении газов этот же прирост энтропии происходит за счет ее
генерации внутри системы; никакой работы система при этом не совершает.
После подстановки (2.8) выражение (2.9) можно переписать в виде
 . (2.10) . (2.10)
Этому соотношению отводится обязательное место в курсах термодинамики ввиду
его кажущейся парадоксальности. Примечательно, что для изменения энтропии (при
смешении идеальных газов!) не имеет значения, что с чем смешивается, а также
при каких давлении и температуре. По существу здесь приведен неформальный вывод
(2.10).
Дополним вывод (2.10) его полезными следствиями. Вводя молярные доли
компонентов  и и  , получим выражение для изменения энтропии в расчете на 1 моль
образующейся смеси: , получим выражение для изменения энтропии в расчете на 1 моль
образующейся смеси:
 . (2.11) . (2.11)
Максимум этой функции приходится на эквимолярную смесь газов,  0.5. 0.5.
С точки зрения теории разделения смесей веществ представляет интерес
проследить изменение производства энтропии при добавлении достаточно большого
числа молей компонента B к одному молю компонента A. Полагая в
(2.10)  и и  , получим , получим
 . (2.12) . (2.12)
При выводе (2.12) использовалось математическое представление
логарифмической функции
 . .
Формула (2.12) показывает, что последовательное разведение смеси  сопровождается
бесконечным ростом энтропии в расчете на моль примесного компонента. сопровождается
бесконечным ростом энтропии в расчете на моль примесного компонента.
Формула (2.10) дает интегральную величину приращения энтропии при смешении
конечных количеств газа. Для того, чтобы придти к компактному дифференциальному
выражению, аналогичному формуле (2.7) для теплообмена, видоизменим модель
смешения компонентов (см. рис. 2.4). Будем предполагать, что смешение
происходит через проницаемую для обоих компонентов мембрану, либо через
достаточно узкий вентиль, разделяющие сосуды, заполненные смесями A и B
разного состава. Система термостатирована, и в обоих сосудах при помощи поршней
поддерживается постоянное давление p. При ограниченной скорости
смешения состав смеси в каждом из сосудов может считаться однородным по объему
сосуда. Таким образом, данная система аналогична теплообменной системе со
слабопроводящей перегородкой.

Рис.2.4. Самопроизвольное смешение
веществ A и B в системе с узким вентилем.
Пусть  и и  – текущие
значения химических потенциалов компонентов A и B в первом
сосуде; – текущие
значения химических потенциалов компонентов A и B в первом
сосуде;  и и  – их значения во
втором сосуде. Для определенности предположим, что составы смесей таковы, что – их значения во
втором сосуде. Для определенности предположим, что составы смесей таковы, что  и соответственно и соответственно
 .
Следовательно, компонент A диффундирует из первого сосуда во второй, а
компонент B – в противоположном направлении. .
Следовательно, компонент A диффундирует из первого сосуда во второй, а
компонент B – в противоположном направлении.
Дифференциальное изменение энтропии при переносе в противоположных
направлениях малых количеств компонентов  и и  рассчитаем прямым путем, через изменение
функции Гиббса, с помощью соотношения рассчитаем прямым путем, через изменение
функции Гиббса, с помощью соотношения   . Поскольку давление в системе постоянное,
имеем . Поскольку давление в системе постоянное,
имеем  . Это
равенство определяет равновесную составляющую изменения энтропии.
Следовательно, . Это
равенство определяет равновесную составляющую изменения энтропии.
Следовательно,  . Так как . Так как  есть парциальное значение функции Гиббса для i-го
компонента, для рассматриваемого изобарно-изотермического процесса смешения
справедливо есть парциальное значение функции Гиббса для i-го
компонента, для рассматриваемого изобарно-изотермического процесса смешения
справедливо
 , ,
где  и и  – изменения
функций Гиббса для первой и второй частей системы; – изменения
функций Гиббса для первой и второй частей системы;  и и  (знаки (знаки  и и  определены относительно первого
сосуда). Отсюда определены относительно первого
сосуда). Отсюда
 . (2.13) . (2.13)
Отметим, что по общим условиям вывода полученное выражение справедливо для
изобарно-изотермического смешения не только идеальных газов, но и неидеальных
газов и жидкостей.
|


 . (2.10)
. (2.10) . (2.12)
. (2.12) .
.