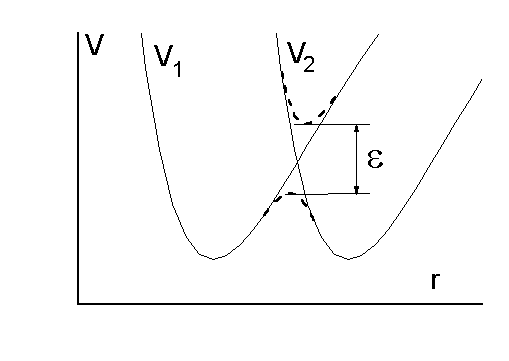
Лекция 2. Качественное рассмотрение поверхности потенциальной энергии
2.1 Адиабатическое расщепление
В ходе приведенного выше рассмотрения мы видели, что наличие обменного взаимодействия приводит к возникновению поверхности потенциальной энергии системы атомов. Возникает два связанных между собой вопроса: 1) всегда ли химическая реакция протекает как движение изображающей точки по такой поверхности, т.е. всегда ли возможно адиабатическое протекание реакции? 2) какова величина энергетического барьера реакции при адиабатическом процессе? Исчерпывающим ответ на эти вопросы можно получить, если известны поверхности потенциальной энергии для каждого из возможных электронных состояний системы. Если эти поверхности находятся по энергии достаточно далеко друг от друга (энергетический зазор между ними велик на всем пути реакции), влиянием верхних электронных состояний на протекание реакции можно пренебречь. Высота точки перевала на поверхности является в этом случае энергией активации реакции. Однако количественные расчеты такого рода для реально изучаемых систем - достаточно трудное дело. Поэтому посмотрим, какие ответы на эти вопросы можно получить из качественного анализа.
Рассмотрим молекулярную систему, имеющую два различных состояния. Каждое из этих состояний, рассмотренное без учета взаимного влияния, называется "диабатическим" термом. Пусть диабатические термы двух возможных состояний системы пересекаются (Рис.2.1).

Такими состояниями могут быть два различных электронных состояния молекулы или состояние исходных реагентов и продуктов химической реакции. Для решения вопроса, будут ли эти два состояния смешиваться и образовывать единую поверхность потенциальной энергии, используем широко распространенный в квантовой механике прием, который называется теорией возмущений.
Его суть заключается в следующем. Пусть
известно точное решение уравнения Шредингера
для какой-то системы, т.е. известен гамильтониан и
соответствующие волновые функции: ![]()
Теперь мы хотим учесть малое возмущение - небольшой дополнительный вклад в гамильтониан, т.е. некоторое взаимодействие с небольшой энергией. Составим новый гамильтониан в виде:
![]() (2.1)
(2.1)
где ![]() - возмущение,
- возмущение, ![]() - малый параметр.
- малый параметр.
Будем искать новые собственные функции и собственные значения для возмущенной системы, раскладывая их в степенной ряд по параметру:
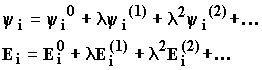 (2.2)
(2.2)
Если мы ограничимся членами, содержащим ![]() , решение будет
получено в рамках теории возмущения первого
порядка, если сохраним члены с
, решение будет
получено в рамках теории возмущения первого
порядка, если сохраним члены с ![]() 2 , то - теории возмущения второго
порядка. Видно, что член, описывающий возмущение,
должен быть невелик, для того, чтобы степенной
ряд быстро сходился. На практике теорию
возмущений более второго порядка используют
очень редко. Подстановка (2.2) в (2.1) приводит к
системам уравнений, с помощью которых и
получается окончательное решение для
возмущенной системы.
2 , то - теории возмущения второго
порядка. Видно, что член, описывающий возмущение,
должен быть невелик, для того, чтобы степенной
ряд быстро сходился. На практике теорию
возмущений более второго порядка используют
очень редко. Подстановка (2.2) в (2.1) приводит к
системам уравнений, с помощью которых и
получается окончательное решение для
возмущенной системы.
В рассматриваемом случае пусть y 1 и y 2 - точные собственные волновые функции гамильтониана, соответствующие первому и второму состояниям системы, а E1 и E2 - их собственные значения. Результат взаимного влияния этих двух термов будем искать как волновую функцию, составленную из волновых функций отдельных состояний:
![]() (2.3)
(2.3)
Малым возмущением является сдвиг ![]() r из положения,
выбранного нами в качестве известного:
r из положения,
выбранного нами в качестве известного:
![]() , (2.4)
, (2.4)
Подстановка (2.3) в уравнение Шредингера с учетом возмущения
![]()
приводит к уравнению
![]() (2.4)
(2.4)
Это уравнение домножается слева на ![]() и интегрируется, а затем
на
и интегрируется, а затем
на ![]() и также
интегрируется. В результате получается система
секулярных уравнений:
и также
интегрируется. В результате получается система
секулярных уравнений:
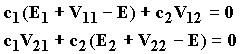 (2.5)
(2.5)
где:
V11 = < ![]() 1
1![]()
![]()
![]()
![]() 1>
1>
V12 = V21 = <![]() 1
1![]()
![]()
![]()
![]() 2>
(2.6)
2>
(2.6)
V22 = <![]() 2
2![]()
![]()
![]()
![]() 2>
2>
которые имеют нетривиальное решение при равенстве нулю соответствующего определителя. Из этого условия находится значение энергии уровней:
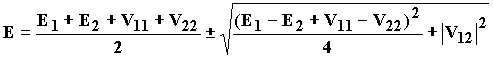 (2.7)
(2.7)
Величина ![]() V12
V12![]() 2 =
2 =![]() 2 называется адиабатическим
расщеплением. Корень из этой величины равен
энергетической щели между образовавшимися
адиабатическими термами (Рис. 2.1). Таким образом,
величина расщепления между пересекающимися
термами и сама возможность пересечения
определяется величиной интеграла
2 называется адиабатическим
расщеплением. Корень из этой величины равен
энергетической щели между образовавшимися
адиабатическими термами (Рис. 2.1). Таким образом,
величина расщепления между пересекающимися
термами и сама возможность пересечения
определяется величиной интеграла
V12 = <![]() 1
1![]()
![]()
![]()
![]() 2>
(2.8)
2>
(2.8)
Вспомним, что волновые функции можно
представить как произведения спиновых,
электронных, колебательных и т.д. сомножителей.
Смещение по координате терма всегда
полносиметрично, т.е. оператор ![]() - полносиметричен. Отсюда следует, что
если
- полносиметричен. Отсюда следует, что
если ![]() 1 и
1 и ![]() 2 соответствуют
состояниям с различным спином, то интеграл (2.8)
равен нулю. Эти состояния не смешиваются, и
переход между ними не происходит. Такие переходы
называют запрещенными по спину. Если волновые
функции
2 соответствуют
состояниям с различным спином, то интеграл (2.8)
равен нулю. Эти состояния не смешиваются, и
переход между ними не происходит. Такие переходы
называют запрещенными по спину. Если волновые
функции ![]() 1 и
1 и ![]() 2 имеют
различную симметрию, то интеграл (2.8) также равен
нулю. Таким образом, взаимодействие между
состояниями и переход системы из одного
состояния в другое будут запрещены по симметрии.
Большое расщепление между термами будет
наблюдаться, если функции
2 имеют
различную симметрию, то интеграл (2.8) также равен
нулю. Таким образом, взаимодействие между
состояниями и переход системы из одного
состояния в другое будут запрещены по симметрии.
Большое расщепление между термами будет
наблюдаться, если функции ![]() 1 и
1 и ![]() 2
имеют одинаковую симметрию. В этом случае из
исходных термов образуется два новых терма,
движение по которым можно рассматривать как
адиабатическое. Это заключение имеет название
"правила непересечения термов одинаковой
симметрии". В многоатомных молекулах интеграл
(2.8) может быть близок к нулю также в связи с малым
перекрыванием y
2
имеют одинаковую симметрию. В этом случае из
исходных термов образуется два новых терма,
движение по которым можно рассматривать как
адиабатическое. Это заключение имеет название
"правила непересечения термов одинаковой
симметрии". В многоатомных молекулах интеграл
(2.8) может быть близок к нулю также в связи с малым
перекрыванием y ![]() 1 и
1 и ![]() 2,
даже когда они имеют одинаковую симметрию и спин.
2,
даже когда они имеют одинаковую симметрию и спин.
Полученные нами запреты по спину и по симметрии не являются абсолютными. Действительно, если принять во внимание спин-орбитальное взаимодействие, то разделение волновой функции на спиновую и орбитальную часть становится неправомочным. Точно так же не является строгим разделение волновой функции на электронную и колебательную. Таким образом, для состояний, различающихся по симметрии или по спину, интеграл (2.8) является малым, но не точно равным нулю. Это означает, что любые два пересекающихся терма взаимодействуют между собой и образуют два новых терма. Однако величина расщепления между ними в силу запретов по симметрии или по спину может быть малой величиной. Поэтому пересечения термов часто называют квазипересечением.
2.2 Неадиабатические переходы
Рассмотрим случай, когда взаимодействие между двумя термами невелико (случай малого расщепления). В этих условиях нельзя рассматривать поведение системы как адиабатическое. Движение изображающей точки может происходить как по исходному терму, так и с переходом на другой терм. (Рис.2.1). Рассчитать вероятность перехода системы с одного терма на другой для реальных систем в многомерном пространстве достаточно сложно. Часто эту задачу решают, опираясь на аналогию с двухатомной молекулой, для которой рассмотрение этого вопроса привело к решению, которое носит имя Ландау-Зинера. В этом решении вероятность остаться на нижней поверхности потенциальной энергии, т.е. перейти с одного диабатического терма на другой, выражается формулой:
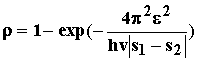 (2.9)
(2.9)
где ![]() 2 -
адиабатическое расщепление, v -скорость
движения изображающей точки в области
квазипересечения,
2 -
адиабатическое расщепление, v -скорость
движения изображающей точки в области
квазипересечения,
![]() s1
- s2
s1
- s2![]() =
=![]()
![]() V1 - V2
V1 - V2![]() -
разность углов наклона диабатических термов в
точке пересечения. Если величина
-
разность углов наклона диабатических термов в
точке пересечения. Если величина ![]() не слишком далека от нуля
(показатель степени в экспоненте мал), то
разлагая в ряд получим:
не слишком далека от нуля
(показатель степени в экспоненте мал), то
разлагая в ряд получим:
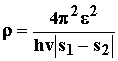 (2.10)
(2.10)
Видно, что вероятность для системы остаться на
диабатическом терме, равная 1-![]() , растет с увеличением скорости
движения системы в области квазипересечения.
, растет с увеличением скорости
движения системы в области квазипересечения.
Усредняя эту формулу по распределению Максвелла-Больцмана для импульсов (скоростей) при заданной температуре, получаем:
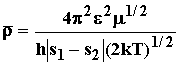 (2.11)
(2.11)
где ![]() - приведенная
масса системы.
- приведенная
масса системы.
В качестве примера реакции, в ходе которой необходимо учитывать переход с одного терма на другой, рассмотрим реакцию в газовой фазе между атомом активного металла M и молекулой галогена Hal2. Известно, что большое сечение этой реакции объясняется так называемым "гарпунным механизмом", который предполагает перенос электрона с атома металла на молекулу галогена, притяжение получающихся ионов за счет кулоновского взаимодействия и затем распад образующегося комплекса:
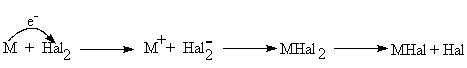
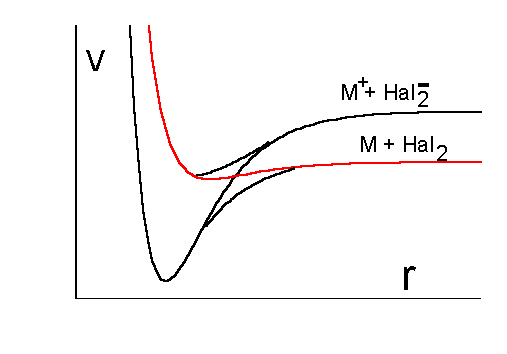
Соответствующие этой реакции термы показаны на Рис.2.2. Терм, отвечающий за столкновение незаряженных частиц, пересекается с термом описывающим столкновению ионов.
В области пересечения термов может происходить переход от неполярного к ионному состоянию пары реагентов, т.е. перенос электрона. Вероятность этого процесса может быть оценена по формулам (2.9) - (2.11).
2.3 Правила симметрии
Полученные нами выше выводы имеют весьма общий характер. Они применимы к проблемам спектроскопии, фотохимии и т.п. Вернемся, однако, к рассмотрению вида поверхности потенциальной энергии, соответствующей реакции многоатомной молекулы.
Запрет по спину требует, чтобы суммарный спин исходных веществ равнялся суммарному спину продуктов реакции. Это требование накладывает некоторые ограничения на типы возможных элементарных актов реакции. Однако большинство возможных реакций удовлетворяет требованию сохранения суммарного спина реагирующей системы.
Использовать симметрию молекул для предсказания вида поверхности потенциальной энергии несколько сложнее. Основное состояние всех молекул естественно является полносимметричным в соответствующих группах симметрии, поскольку собственно группа симметрии определяется геометрией молекулы. С другой стороны, различные молекулярные орбитали одной и той же молекулы имеют различную симметрию. Теоретическое рассмотрение ограничений, накладываемых на элементарный акт реакции этим обстоятельством, привело к формулировке принципа сохранения орбитальной симметрии. Наибольший вклад в его разработку внесли Вудворд и Хофман. В соответствии со своим названием, этот принцип гласит, что симметрия молекулярных орбиталей не изменяется на всем пути реакции.
Проиллюстрируем применение принципа сохранения орбитальной симметрии для определения возможности протекания элементарного акта реакции на простом примере парного обмена атомов в двух молекулах водорода.
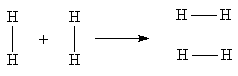
Предположим плоское переходное состояние для этой реакции (Рис.2.3). Четыре атома водорода имеют четыре s-электрона. Реагирующая система имеет точечную группу симметрии D2h. В соответствии с этой группой можно классифицировать четыре молекулярные орбитали для исходного и конечного состояний системы (Рис. 2.4).
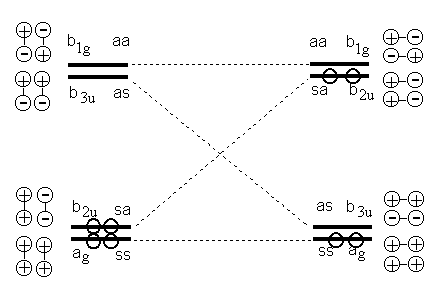
Рис.2.4. называется корреляционной диаграммой молекулярных орбиталей. Он показывает, что одной из связывающих молекулярных орбиталей реагентов соответствует (коррелирует по симметрии) разрыхляющая молекулярная орбиталь продуктов реакции. Таким образом, требование сохранения орбитальной симметрии приводит к выводу, что в ходе реакции должны образоваться продукты в дважды возбужденном электронном состоянии. Очевидно, что такая реакция была бы энергетически совершенно невозможна. Дополнительные важные выводы можно сделать, если от рассмотрения корреляционной диаграммы орбиталей перейти к рассмотрению корреляционной диаграммы состояний исходных реагентов и продуктов реакции (Рис.2.5). На этом рисунке показано качественное расположение по энергии некоторых электронных состояний рассматриваемой системы. Линии, показывающие корреляцию состояний, проведены на основании корреляционной диаграммы орбиталей. Эти линии качественно показывают, как изменяется (растет, уменьшается или остается приблизительно постоянной) энергия электронных состояний при движении системы по координате реакции. Это означает, что корреляционная диаграмма состояний представляет собой сильно упрощенное и искаженное по масштабам, однако сохраняющее основные топологические свойства, сечение поверхностей потенциальной энергии системы вдоль координаты реакции. Из диаграммы видно, что основное состояние как исходных реагентов, так и продуктов реакции полносимметрично.

Это означает, что линия, связывающая основное состояние реагентов с дважды возбужденным состоянием продуктов реакции, отвечает состоянию той же симметрии, что и линия, связывающая дважды возбужденное состояние реагентов и основное состояние продуктов реакции. Как мы уже знаем, такие состояния не могут быть вырожденными, т.е. соответствующие линии не могут пересекаться (правило непересечения термов одинаковой симметрии). Отсюда следует вывод, что в действительности эти два состояния в области пересечения смешиваются между собой и образуют два новых терма, разделенных энергией адиабатического расщепления. Значит, рассматриваемая реакция может протекать адиабатически, т.е. оставаясь на нижней поверхности потенциальной энергии. Однако энергетический барьер для реакции, т.е. энергия активации, тем не менее останется настолько большим, что в реальности наблюдать реакцию по рассмотренному механизму нельзя. Такие реакции, энергия активации которых велика в результате ограничений, накладываемых симметрией молекулярных орбиталей, называются реакциями, запрещенными по орбитальной симметрии.
Рис.2.5 показывает также, что одно из однократно возбужденных состояний реагентов коррелирует с однократно возбужденным состоянием продуктов реакции. Это говорит о разрешенности реакции в этом состоянии, т.е. о возможности ее протекания при поглощении кванта света.
При анализе симметрии орбиталей мы
пользовались их классификацией в соответствии с
точечной группой симметрии. При этом
учитывается, как меняются молекулярные орбитали
при действии всех элементов симметрии
реагирующей молекулярной системы. В таком
строгом подходе, однако, нет необходимости. В
действительности многие элементы симметрии
можно сразу исключить из рассмотрения, поскольку
они не изменяются в ходе реакции. Таким элементом
в рассмотренной реакции является, например,
плоскость симметрии, проходящая через все атомы
водорода. Исключая из рассмотрения лишние
элементы симметрии, можно значительно сократить
трудоемкость описанной процедуры. В
рассмотриваемой реакции достаточным
оказывается рассмотрение только двух элементов
симметрии - двух плоскостей ![]() 1 и
1 и ![]() 2,
показанных на Рис.2.6
2,
показанных на Рис.2.6
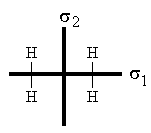
Относительно этих двух плоскостей симметрии легко произвести классификацию молекулярных орбиталей, отмечая буквой s асимметричные и буквой a - антисимметричные орбитали. Такая классификация показана на Рис. 2.4. Она позволяет получить совершенно такие же выводы о виде корреляционных диаграмм орбиталей и корреляционных диаграмм электронных состояний, как и классификация, основанная на рассмотрении группы симметрии.
Рассмотрение корреляционных диаграмм позволяет определять возможность протекания многих элементарных реакции. Поэтому сформулируем стадии такого рассмотрения, иллюстрируя их на примере реакции циклизации бутадиена в циклобутен (Рис. 2.7).
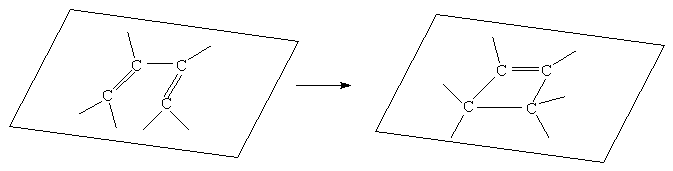
Стадия 1. В молекулах исходного вещества и
продукта реакции выделяются связывающие и
разрыхляющие молекулярные орбитали, которые
изменяются в ходе процесса. В рассматриваемом
случае это - орбитали бутадиена, образующие ![]() - связи, и образующаяся
из них
- связи, и образующаяся
из них ![]() - связь
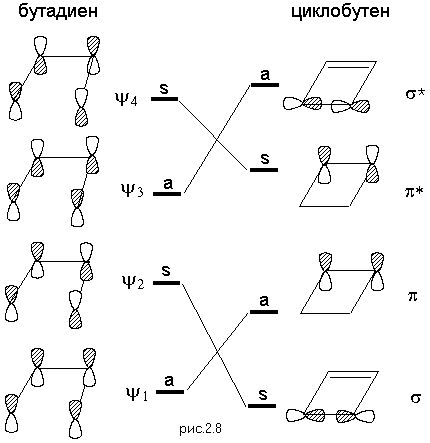
молекулы циклобутена (Рис.2.8).
- связь
молекулы циклобутена (Рис.2.8).
Стадия 2. Качественно определяется относительное расположение молекулярных орбиталей по энергии. Если между атомами лежит узел орбитали, орбиталь является разрыхляющей. Энергия разрыхляющей орбитали значительно выше энергии связывающих орбиталей.
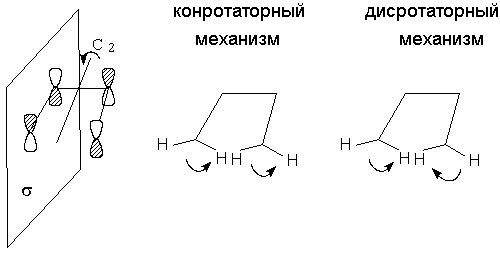
Стадия 3. Определяются элементы симметрии
системы. Выбирается рассматриваемый механизм
реакции и выясняется, какие элементы симметрии
сохраняются в ходе этого механизма. В
рассматриваемом примере исходная молекула и
продукт реакции имеют ось симметрии второго
порядка и плоскость симметрии, проходящие через
середины центральной C-C связи. Можно представить
себе два механизма реакции - конротаторный и
дисротаторный. Они различаются тем, в одну и ту же
или в разные стороны вращаются p-орбитали (и
соответственно C-H связи у концевых атомов
углерода) в ходе реакции. В первом случае в ходе
элементарного акта сохраняется ось второго
порядка C2, а во втором случае сохраняется
плоскость симметрии ![]() . (Рис.2.9).
. (Рис.2.9).
Стадия 4. Производится классификация орбиталей относительно элементов симметрии. Если при действии элемента симметрии знак волновой функции меняется на противоположный - орбиталь антисимметрична относительно этого элемента, если знак сохраняется, орбиталь симметрична относительно действующего элемента симметрии. Устанавливается корреляция между молекулярными орбиталями реагентов и продуктов реакции. Корреляционная диаграмма для конротаторного механизма циклизации бутадиена (Рис.2.8) показывает разрешенность реакции.
Стадия 5. При необходимости анализа возможности протекания реакции в различных электронных состояниях реагентов строится корреляционная диаграмма состояний. Для этого молекулярные орбитали заселяются нужным числом электронов, определяется симметрия состояний (в соответствии с правилами: s*s=a*a=s, s*a=a), устанавливается их корреляция и производится адиабатическое расщепление состояний с одинаковой симметрией.
Ограничения, накладываемые орбитальной симметрией на возможность протекания элементарных актов реакции, позволяют сформулировать некоторые правила. В частности, достаточно простые правила Вудворда-Хофмана позволяют определить разрешенность по симметрии перициклических реакций, т.е. реакций, протекающих через циклические переходные состояния. Заинтересованный читатель может найти эти правила в дополнительной литературе. Мы же отметим только, что практически всегда являются запрещенными в основном состоянии реакции, протекающие через плоские четырехчленные переходные состояния.
Этот запрет, однако, нарушается в случае
протекания реакции через неплоские
четырехчленные циклы. Разрешенными являются
также реакции, протекающие по ионному механизму,
в частности реакция KJ + CsCl ![]() KCl + CsJ
KCl + CsJ
может протекать через четырехчленное переходное состояние. Причина этого заключается в том, что орбитальную симметрию имеет смысл рассматривать, когда рвутся или образуются направленные ковалентные связи. Ионные же соединения в последнем примере не имеют направленных связей и поэтому такие реакции разрешены.
Протекание реакции с плоскими шестичленными переходными состояниями, как правило, разрешено в основном состоянии. Именно это является причиной большого числа таких реакций органических соединений.
Существенным ограничением применимости анализа элементарных актов реакции на основе симметрии является то, что большинство сложных молекул не имеют ни одного элемента симметрии. Особенно часто несимметричными являются переходные состояния, поскольку в них, как правило, участвуют две различные молекулы. Однако ситуация в таких случаях не так плоха, как может показаться на первый взгляд. Действительно, в реакции обычно разрываются и образуются вновь не все химические связи реагентов. Таким образом, всегда можно выбрать реакционный центр, который претерпевает реакцию, и более или менее инертные в рассматриваемой реакции заместители. Если отвлечься от химической структуры заместителей, то симметрия реакции станет значительно выше и рассмотренные нами методы анализа могут быть с успехом применены.. Конечно, влиянием заместителей на протекание реакции полностью пренебрегать нельзя. Именно поэтому в химической литературе можно встретить выражение "реакция, частично запрещенная по симметрии". В качестве примера такой реакции приведем реакцию цис-присоединения молекулы HCl к этилену. Если бы присоединяющаяся молекула была гомоядерной, такая реакция через плоский четырехчленный цикл была бы запрещена. Молекула HCl нарушает симметрию переходного состояния. Несмотря на это, реакция цис-присоединения остается в значительной степени запрещенной.
Приведенные примеры касались элементарных реакций, которые мы ранее классифицировали как реакции типа изомеризации и перегруппировки, а также как реакции диссоциации/рекомбинации. Остальные упомянутые нами типы элементарных актов реакции обычно не рассматривают с точки зрения симметрии. Это связано с тем, что реакции обмена и реакции переноса электрона всегда разрешены по орбитальной симметрии.
2.4 Многомерные поверхности потенциальной энергии. Конические пересечения
Большинство выводов, которые мы получили, основывались на рассмотрении одномерных термов, показанных на Рис.2.1. Реальные молекулярные системы имеют значительно большее число независимых координат, и, соответственно, их термы представляют собой многомерные гиперповерхности. Это обстоятельство несколько усложняет ответ на вопрос: пересекаются или не пересекаются две поверхности потенциальной энергии реальной молекулярной системы, и, соответственно, ответ на вопрос об адиабатичности той или иной реакции. Известно, что если в конфигурационном пространстве размерности S пересекаются два терма Un и Um размерности S, отвечающие электронным состояниям различной симметрии, то эти термы могут пересекаться по многообразию (S-1). Это означает, что одномерные термы (двухатомная молекула) разной симметрии пересекаются в точке (S-1=0), двумерные термы - по линии (S-1=1) и т.д.
Если же Un и Um отвечают электронным состояниям одинаковой симметрии, то они могут пересекаться по (S-2)-мерному многообразию. Для одномерных термов, следовательно, пересечения не может быть вообще, двумерные термы могут в этом случае иметь одну общую точку, трехмерные термы могут иметь общую линию и.т.п. Точка пересечения двух двумерных потенциальных поверхностей является вершиной пары эллиптических конусов, которые соответствуют образующимся из исходных термов адиабатическим поверхностям потенциальной энергии (Рис. 2.10).
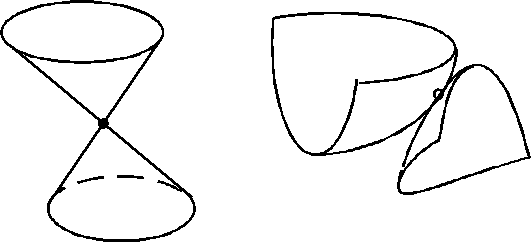
В связи с этим такие особенности поверхностей потенциальной энергии носят название конических пересечений (conical intersections).
Рассмотрение конических пересечений ППЭ
особенно полезно при исследовании
фотохимических процессов, которые всегда
включают в себя переход с нижней на более высоко
лежащую поверхность потенциальной энергии
(процесс возбуждения) и обратный переход
(процессы электронной релаксации и образования
продуктов реакции). Рассмотрим в качестве
примера реакцию фотоизомеризации этилена.
Известно, что основное электронное состояние
этой молекулы отвечает равновесной плоской
геометрии, т.е. угол q между двумя плоскостями,
заданными CH2-группами, равен нулю. Если
рассматривать одномерные термы, считая
координатой реакции угол ![]() , оказывается, что в
возбужденном состоянии равновесной геометрией
является "свернутая" конфигурация, т.е.
минимум терма отвечает углу
, оказывается, что в
возбужденном состоянии равновесной геометрией
является "свернутая" конфигурация, т.е.
минимум терма отвечает углу ![]() =
=![]() /2 (Рис.2.11)
/2 (Рис.2.11)
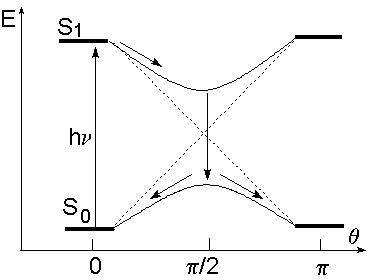
Основное и возбужденное электронные состояния молекулы сильно отличаются по энергии, т. е. адиабатическое расщепление термов, приведенных на рисунке, велико. Оценка вероятности прохождения системы по диабатическому терму из исходно возбужденного состояния непосредственно в основное состояние продукта реакции, которое можно произвести по формуле Ландау-Зиннера (2.9), показывает, что таким процессом можно пренебречь (вероятность составляет величину ~10-21). В связи с этим, реакцию обычно рассматривают, как квантовый переход с верхней на нижнюю поверхности потенциальной энергии, показанный на рисунке 2.11 стрелками.
Такой вывод, однако, противоречит экспериментальным наблюдениям, показывающим, что время протекания элементарного акта реакции составляет несколько десятков фемтосекунд, т.е. реакция происходит слишком быстро, чтобы включать в себя стадию электронной релаксации. Действительно, переход из электронно-возбужденного состояния в основное состояние при значительной величине энергетической щели должен занимать время порядка наносекунд.
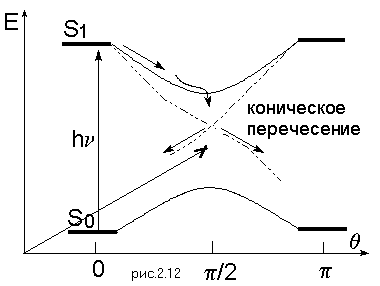
Объяснение этого противоречия можно получить, если рассмотреть многомерные термы вместо одномерных. Оказывается, что поверхности потенциальной энергии возбужденного и основного состояний имеют коническое квазипересечение в стороне от выбранной нами координаты реакции. Это означает, что движение по другой координате ведет к понижению поверхности возбужденного состояния до ее пересечения с поверхностью основного состояния, как это схематически показано на рис.2.12.
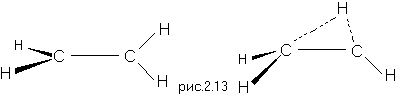
Таким образом, в ходе элементарного акта реакции система через коническое пересечение непосредственно переходит с поверхности потенциальной энергии возбужденного состояния на поверхность потенциальной энергии основного состояния. Координата, движение по которой ведет в область конического пересечения, однозначно может быть определена только квантово-химическими расчетами хорошего уровня. В рассматриваемом случае такой координатой оказалось смещение заместителя от одного атома углерода к другому, как это показано на Рис.2.13. В настоящее время реальность такого механизма проверяется по своим стереохимическим следствиям в случае замещенных молекул этилена, а также по результатам фемтосекундных экспериментов.
2.5 Полуэмпирические методы построения поверхности потенциальной энергии
Качественная информация о форме поверхности потенциальной энергии в области пути реакции, которая может быть получена из рассмотрения симметрии системы, часто недостаточна для обоснованных выводов о детальном механизме реакции. С другой стороны, строгий расчет до настоящего времени остается настолько сложной и дорогостоящей задачей, что он применяется лишь к небольшой части наиболее простых реакций. В связи с этим очень часто задача описания ППЭ решается полуэмпирическими методами. Расчеты ab initio при этом используются для определения или уточнения параметров полуэмпирических моделей в нескольких точках поверхности потенциальной энергии. Исторически наиболее ранним методом полуэмпирического расчета ППЭ является Метод ЛЭПС (Лондон-Эйринг-Поляни-Сато). Он заключается в использовании формулы Гайтлера-Лондона для двухатомной молекулы или ее обобщения на случай трех, четырех и т.д. атомов:
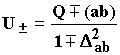 (2.12)
(2.12)
В этой формуле содержатся кулоновский Q,
обменный (ab) интегралы и интеграл
перекрывания ![]() .
Идея метода заключается в оценке этих интегралов
с использованием данных эксперимента.
Действительно, в спектроскопии двухатомных
молекул установлено, что энергия двухатомных
молекул приближенно описывается функцией Морзе:
.
Идея метода заключается в оценке этих интегралов
с использованием данных эксперимента.
Действительно, в спектроскопии двухатомных
молекул установлено, что энергия двухатомных
молекул приближенно описывается функцией Морзе:
![]() (2.13)
(2.13)
где Dab - энергия связи, xab=rab - roab
- отклонение длины связи от равновесной величины,
![]() ab -
постоянная, характеризующая ширину
потенциальной ямы.
ab -
постоянная, характеризующая ширину
потенциальной ямы.
Численные значения величин Dab и ![]() ab определяются
так, чтобы частоты колебаний молекулы и ее
энергия диссоциации соответствовали
эксперименту. Приравнивая энергии в формулах (2.12)
и (2.13), можно определить один из неизвестных
интегралов в формуле Гайтлера-Лондона.
Первоначально предполагалось равенство нулю
интеграла перекрывания, и на основании точных
расчетов для молекулы водорода отношение
кулоновского и обменного интегралов считалось
постоянным. Таким образом, оставался только один
неизвестный параметр, который и определялся с
использованием спектроскопических данных. Как
оказалось, полученная в этом приближении
поверхность потенциальной энергии для трех
атомов имеет особенность, которую не
подтверждает ни эксперимент, ни расчеты ab initio.
Это "озеро Эйринга" - небольшой
потенциальный минимум на поверхности
потенциальной энергии вблизи вершины барьера.
(Рис. 1.6). Для того, чтобы более точно описать ППЭ,
C.Сато предложил усовершенствовать метод и
использовать спектроскопические данные не
только о связывающем терме двухатомной молекулы,
но и ее диссоциативном терме, который также
неплохо известен. Он предложил описывать
диссоциативный терм формулой, аналогичной
функции Морзе (функция анти-Морзе):
ab определяются
так, чтобы частоты колебаний молекулы и ее
энергия диссоциации соответствовали
эксперименту. Приравнивая энергии в формулах (2.12)
и (2.13), можно определить один из неизвестных
интегралов в формуле Гайтлера-Лондона.
Первоначально предполагалось равенство нулю
интеграла перекрывания, и на основании точных
расчетов для молекулы водорода отношение
кулоновского и обменного интегралов считалось
постоянным. Таким образом, оставался только один
неизвестный параметр, который и определялся с
использованием спектроскопических данных. Как
оказалось, полученная в этом приближении
поверхность потенциальной энергии для трех
атомов имеет особенность, которую не
подтверждает ни эксперимент, ни расчеты ab initio.
Это "озеро Эйринга" - небольшой
потенциальный минимум на поверхности
потенциальной энергии вблизи вершины барьера.
(Рис. 1.6). Для того, чтобы более точно описать ППЭ,
C.Сато предложил усовершенствовать метод и
использовать спектроскопические данные не
только о связывающем терме двухатомной молекулы,
но и ее диссоциативном терме, который также
неплохо известен. Он предложил описывать
диссоциативный терм формулой, аналогичной
функции Морзе (функция анти-Морзе):
![]() (2.14)
(2.14)
которая, однако, может содержать другую
постоянную ![]() .Таким
образом, появляется два уравнения, из которых
однозначно определяются как кулоновский, так и
обменный интегралы. При этом интеграл
перекрывания было предложено считать
постоянным, независящим от расстояния между
атомами, и использовать как подгоночный
параметр. В результате, используется следующая
формула для потенциала многоатомной молекулы:
.Таким
образом, появляется два уравнения, из которых
однозначно определяются как кулоновский, так и
обменный интегралы. При этом интеграл
перекрывания было предложено считать
постоянным, независящим от расстояния между
атомами, и использовать как подгоночный
параметр. В результате, используется следующая
формула для потенциала многоатомной молекулы:
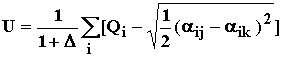 (2.15)
(2.15)
где ![]() - обменный
интеграл.
- обменный
интеграл.
Используя экспериментальные величины или данные, полученные неэмпирическим расчетом для всех пар атомов, входящих в молекулу, можно строить ППЭ для сложных систем.
Одно из направлений дальнейшего развития полуэмпирических методов связано с использованием не одноэлектронных функций, как мы это делали раньше, а многоэлектронных волновых функций для атомов в определенном электронном состоянии и для двухатомных фрагментов. Этот метод (двухатомных фрагментов в молекуле - ДФВМ, Diatomics-in-Molecules - DIM) основан на представлении гамильтониана в виде комбинации атомарных гамильтонианов H i и гамильтонианов двухатомных фрагментов H ij:
![]() (2.16)
(2.16)
где суммирование производится по всем N атомам системы.
На этих примерах хорошо видна тенденция развития полуэмпирических методов расчета в квантовой химии. В качестве основы эти методы используют более или менее строгие формулы, полученные, однако, в достаточно грубых приближениях. Для применения формул параметры в них не рассчитываются строго, а оцениваются из эксперимента. Для компенсации недостатков описания вводятся эмпирические коэффициенты. Несмотря на простоту таких методов, они могут давать весьма ценную информацию, если для определения эмпирических параметров (параметризации) использованы достаточно надежные и многочисленные данные. Можно сказать, что полуэмпирические методы пытаются использовать как теорию, так и богатый экспериментальный материал, накопленный химиками.
Кроме полуэмпирических методов, разработан
также целый ряд практически полностью
эмпирических методов построения ППЭ. К таким
методам, например, относится метод выключающих
функций. Простейший возможный потенциал для
реакции A+BC![]() AB+C в
методе выключающих функций имеет вид:
AB+C в
методе выключающих функций имеет вид:
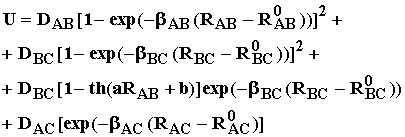 (2.17)
(2.17)
где первый член соответствует связанному состоянию AB, второй - связанному состоянию ВС, третий - выключающая функция, описывающая разрыв связи BC при приближении атома A, и четвертый член описывает отталкивание крайних атомов. Эмпирические параметры a и b описывают скорость ослабления связи BC и расстояние, на котором оно происходит.
Еще один эмпирический метод построения поверхности потенциальной энергии известен под названием BEBO (bond energy - bond order, энергия связи - порядок связи). Идея метода состоит в том, что в ходе реакции сохраняется суммарный порядок разрываемой и образующейся связи. В качестве отправной точки использована эмпирическая зависимость, найденная Поляни:
![]() (2.18)
(2.18)
где R - расстояние между атомами, n - порядок связи.
Будем считать, что эта формула справедлива не только в равновесной конфигурации молекулы, но и на всем пути реакции. Одновременно примем, что порядок связи n может принимать не только целочисленные значения. Тогда для реакции AB+C запишем:
![]()
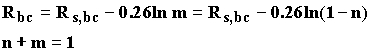 (2.19)
(2.19)
где n и m - порядки связей AB и BC, Rs - равновесные длины этих связей..
Поскольку в ходе элементарного акта порядок разрываемой связи n меняется от 0 до 1, то полученные уравнения в параметрическом виде выражает зависимость Rab и Rbc, т.е. описывают координату реакции.
Для нахождения потенциальной энергии системы вдоль этой координаты используется еще одна эмпирическая зависимость:
![]() (2.20)
(2.20)
где Ds - энергия одинарной связи, p - эмпирический параметр, лежит в интервале 0,8 - 1,09. Чтобы учесть отталкивание несвязанных атомов (A и C в нашем примере) используется потенциал анти-Морзе (2.14).
![]() (2.21)
(2.21)
В целом для потенциальной энергии
![]()
подстановка всех членов дает:
![]() (2.22)
(2.22)
Расчет энергетического профиля реакций переноса водорода по формуле (2.22) дает удивительно хорошее согласие с результатами неэмпирических методов. Недостатком метода является то, что его применимость резко падает при удалении от пути реакции.
2.6 Задачи
1. Приведите примеры реакций, запрещенных по спину.
2. Покажите, что протекание реакции циклизации бутадиена в циклобутен в соответствии с дисротаторным механизмом в основном электронном состоянии реагентов запрещено по орбитальной симметрии.
3. Постройте корреляционные диаграммы для реакции циклизации двух молекул этилена с образованием циклобутана. Определите, разрешена ли эта реакция по симметрии.
4. Приведите примеры реакций, протекающих через шестичленное переходное состояние. Покажите разрешенность их по симметрии.
5. Покажите на примере простой реакции обмена отсутствие ограничений по орбитальной симметрии.
6. Оцените величину ![]() в формуле Морзе для какой-нибудь двухатомной
молекулы.
в формуле Морзе для какой-нибудь двухатомной
молекулы.
7. Оцените вероятность адиабатического прохождения (по нижнему терму) реакции в соответствии с Рис. 2.1, считая, что адиабатическое расщепление составляет 12 кДж/моль. Определите, при каком адиабатическом расщеплении прохождением процесса по диабатическому терму можно пренебречь.
8. Определите, разрешено ли протекание следующих элементарных реакций:
a) C2H6 ![]() 2CH3.
2CH3.
b) RH + O2 ![]() ROOH
ROOH
c) 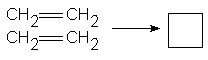
d) 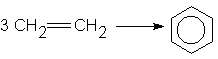
e) H + Cl2 ![]() HCl +Cl
HCl +Cl
9. Оцените энергию активации реакции F + H2 ![]() HF + H по формулам
BEBO,считая. что:
HF + H по формулам
BEBO,считая. что:
DHF=591 кДж/моль, DHH=458 кДж/моль,
![]() HF = 2,219 А-1,
HF = 2,219 А-1, ![]() HH = 1,942 А-1,
HH = 1,942 А-1,
Rs,HF = 0,917 A, Rs,HH = 0,742 A.
Литература.