Лекция 3. Статистическое описание скорости
химической реакции
3.1 Теория переходного состояния
Наиболее строгим теоретическим методом расчета константы скорости химической реакции является расчет траекторий движения изучаемой молекулярной системы по поверхности потенциальной энергии. Поскольку такой расчет производится для одного реакционного комплекса (молекулы, реагирующей пары молекул и т.п.), очевидно, что полученный результат относится к области молекулярной динамики. Он пока мало что может сказать о скорости химической реакции в большом ансамбле частиц. Для перехода от динамики отдельного реакционного комплекса к кинетическим константам, описывающим ансамбль частиц, необходимо:
- задать распределение исходных реагирующих молекул по состояниям (электронным состояниям, скоростям и направлениям взаимного движения двух реагирующих молекул, величинам колебательной и вращательной энергии на каждой из степеней свободы, конформации молекулы);
- рассчитать траектории движения для каждого из состояний в отдельности и получить вероятность протекания реакции в этом состоянии;
- усреднить эти вероятности для получения средней вероятности, которая будет характеризовать кинетическую константу.
Видно, что эта программа весьма трудоемка. Более того, в ходе ее выполнения получается очень большой массив информации о деталях процесса для различных исходных состояний, который затем теряются при усреднении и получении одного числа - константы скорости. Таким образом, расчет кинетических параметров из молекулярно динамических данных представляется очень неэкономичным. В исследовательской практике такие расчеты оправданны, если результаты молекулярной динамики дают качественное объяснение наблюдаемых кинетических закономерностей для целого класса реакций. Они необходимы также для понимания и обработки результатов современного пико- и фемтосекундного эксперимента, результатов исследования элементарного акта методами молекулярных пучков и т.п.
Однако чаще всего оценка кинетической константы химического превращения в газе производится не на основании расчетов молекулярной динамики, а с использованием теории переходного состояния Эйринга-Поляни. Вспомним очень кратко суть этой теории. Из всех особенностей поверхности потенциальной энергии теория переходного состояния использует только одну - величину энергии активации, т.е. высоту энергетического барьера Ea на пути реакции.
Теория основана на двух постулатах:
1. Равновесное максвелл-больмановское распределение молекул реагентов по энергии не нарушается в ходе химической реакции. Из этого постулата следует, что равновесное распределение поддерживается в ходе процесса и в продуктах реакции.
2. Молекулярная система считается прореагировавшей, если она достигла вершины потенциального барьера реакции. Таким образом, движение изображающей точки системы в области переходного состояния является равномерным и прямолинейным. Обратное движение в направлении долины исходных реагентов невозможно.
Постулат о равновесии позволяет определить из термодинамических соображений долю молекул, имеющих энергию, достаточную для преодоления барьера. Например, для реакции
A + B ![]() AB
AB![]()
![]() продукты
продукты
справедливо:
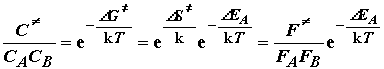 (3.1)
(3.1)
где СA и CB - концентрации исходных реагирующих молекул A и B;
![]() - концентрация
реагирующих пар AB
- концентрация
реагирующих пар AB![]() , имеющих
энергию, достаточную для преодоления барьера;
, имеющих
энергию, достаточную для преодоления барьера;
![]() G
G ![]() ,
, ![]() S
S ![]() ,
, ![]() EA
EA ![]() - свободная
энергия Гиббса, энтропия и энергия активации,
соответственно;
- свободная
энергия Гиббса, энтропия и энергия активации,
соответственно;
FA, FB, ![]() - соответствующие статистические суммы.
- соответствующие статистические суммы.
Считая, что все реакционные комплексы, имеющие достаточную энергию, преодолевают барьер со скоростью, которая определяется температурой, получаем выражение для константы скорости реакции:
![]()
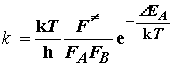 (3.2)
(3.2)
Выделяя из колебательной суммы по состояниям колебательные моды с малой частотой, т.е. наиболее слабые химические связи, будем считать, что именно они претерпевают наибольшие изменения в ходе реакции. Для этих частот сомножители
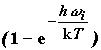 в колебательной
сумме по состояниям можно разложить в ряд,
сохраняя первый член разложения. Скорость
движения изображающей точки на вершине барьера
можно приравнять частоте колебаний в
перевернутом барьере
в колебательной
сумме по состояниям можно разложить в ряд,
сохраняя первый член разложения. Скорость
движения изображающей точки на вершине барьера
можно приравнять частоте колебаний в
перевернутом барьере ![]() . Кривизна пути реакции на ППЭ затрудняет
переход из долины продуктов в долину реагентов,
поскольку появляется вероятность реализации так
называемых возвратных траекторий. Это
траектории, в соответствии с которыми
изображающая точка отражается от барьера,
несмотря на достаточную энергию. Учет таких
траекторий производится введением стерического
фактора q < 1. Тогда константа скорости
химической реакции будет рассчитываться в
соответствии с выражением:
. Кривизна пути реакции на ППЭ затрудняет
переход из долины продуктов в долину реагентов,
поскольку появляется вероятность реализации так
называемых возвратных траекторий. Это
траектории, в соответствии с которыми
изображающая точка отражается от барьера,
несмотря на достаточную энергию. Учет таких
траекторий производится введением стерического
фактора q < 1. Тогда константа скорости
химической реакции будет рассчитываться в
соответствии с выражением:
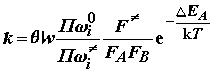 (3.3)
(3.3)
где в суммах по состояниям сохранены вклады от высокочастотных колебаний.
Значительная часть расчетов молекулярной динамики направлена на оценку величины стерического множителя q , входящего в формулу (3.3). Обратим также внимание на то, что в соответствии с формулой (3.3), константа скорости реакции зависит не только от движения по координате реакции, но и от того, насколько сильно изменяются в седловой точке частоты колебаний связей, не затронутых реакцией.
Оценим теперь постулаты теории переходного
состояния. Условие существования
максвелл-больцмановского равновесия означает,
что для частиц с большой энергией уход из долины
реагентов протекает с меньшей скоростью, чем
восстановление числа этих частиц при
молекулярных столкновениях. Это условие можно
сформулировать так: ![]() tr >
tr > ![]() rel, где
rel, где ![]() tr -
характеристическое время исчезновения
реакционных комплексов за счет преодоления
потенциального барьера,
tr -
характеристическое время исчезновения
реакционных комплексов за счет преодоления
потенциального барьера, ![]() rel - время релаксации
максвелл-больцмановского распределения
исходных веществ. Чтобы более точно понять
условия применимости теории переходного
состояния, рассмотрим процессы релаксации
немного подробнее.
rel - время релаксации
максвелл-больцмановского распределения
исходных веществ. Чтобы более точно понять
условия применимости теории переходного
состояния, рассмотрим процессы релаксации
немного подробнее.
3.2 Процессы релаксации
Определим равновесное состояние молекулярной системы как состояние, для которого справедливо максвелл-больцмановское распределение для заселенностей:
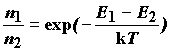 (3.4)
(3.4)
где n1 и n2 - заселенности пары молекулярных состояний (1) и (2). При выполнении этого условия величина T является температурой системы. Под состояниями молекулы можно понимать ее электронное состояние, вращательное состояние, колебательное, спиновое и т.д. Если мы рассматриваем заселенность электронных уровней и убеждаемся в справедливости условия (3.4), то можно говорить об электронной температуре. Если это условие справедливо для заселенностей колебательных уровней, то таким образом определена колебательная температура, и т.д. Таким образом, молекулярную систему можно разделить на подсистемы (электронную, поступательную, колебательную, магнитную и т.д.) и рассматривать наличие равновесия в каждой из этих подсистем. В истинном равновесии температуры всех подсистем должны совпадать. Однако существуют случаи, когда условия равновесия справедливы для отдельных подсистем, но несправедливы для системы в целом. Тогда температуры различных подсистем не равны. В этом случае, а также тогда, когда в какой-либо подсистеме условие равновесия не выполняется, система является неравновесной.
Неравновесная система, на которую не действуют внешние факторы (в замкнутых условиях) самопроизвольно переходит в равновесное состояние. В ходе процесса релаксации к равновесию изменение заселенностей состояний в выбранной подсистеме неравновесной системы обычно происходит экспоненциально. Поэтому можно ввести характеристическое время установления равновесия, которое называют временем релаксации. Для каждой подсистемы характерно свое время релаксации - время электронной релаксации, время колебательной релаксации и т.д. Кроме того, характерное время необходимо для передачи энергии из одной подсистемы в другую, т.е. для установления равновесия между подсистемами, например между электронной и колебательной подсистемой и т.д. Таким образом, любая молекулярная система характеризуется набором времен релаксации. Подсистемы обычно выбирают так, чтобы время релаксации внутри подсистемы было меньше, чем время установления равновесия между подсистемами. Времена релаксации, вообще говоря, могут меняться в очень широких пределах. Например, люминесцентные измерения показывают, что время электронной релаксации молекул может в зависимости от условий составлять от 10-10 до 1 с.
Для теории элементарного акта химической реакции в первую очередь важны релаксационные процессы, которые позволяют молекулам получить энергию, необходимую для преодоления энергетического барьера реакции. Таким образом на скорости протекания химической реакции могут сказаться время установления равновесия по кинетической энергии молекул в газе, время релаксации по колебательным степеням свободы внутри молекулы и между молекулами и в некоторых случаях время вращательной релаксации. В фотохимии, плазмохимии, радиационной химии важнейшую роль играют времена электронной релаксации в молекуле и времена передачи электронной энергии на другие степени свободы.
3.3 Схема Линдемана. Теория Райса-Рамспергера-Касселя-Маркуса (РРКМ)
Наиболее известными моделями, учитывающими процессы релаксации, являются теории мономолекулярных реакций в газе. Действительно, газофазные мономолекулярные реакции при малых давлениях демонстрируют явное отклонение от теории переходного состояния. Эти отклонения проявляются в том, что константа скорости реакции при малых давлениях зависит от давления газа, причем не только от парциального давления реагирующего вещества, но и от давления нереагирующих, инертных веществ. Кроме того, в настоящее время известны реакции, в ходе которых продукты реакции оказываются в сильно возбужденных колебательных состояниях, т.е. демонстрируют явное нарушение постулатов теории переходного состояния.
Зависимость константы скорости газофазной реакции от давления простейшим образом объясняет схема Линдемана. В этой модели учитывается тот факт, что в разреженном газе время передачи колебательной энергии от одной молекулы к другой достаточно велико, поскольку такая передача может происходить только при редких столкновениях молекул. Процесс релаксации по колебательным степеням свободы в модели Линдемана описывается в виде пары процессов, в ходе которых происходит получение и потеря молекулой колебательной энергии, необходимой для преодоления барьера:

Если рассмотреть эту схему в квазиравновесном приближении, мы вернемся к теории переходного состояния. Если же кинетические уравнения, соответствующие этой схеме, решить в квазистационарном приближении относительно концентрации активированных молекул A*, то получится следующее выражение для наблюдаемой скорости реакции:
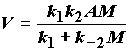 (3.5)
(3.5)
При отсутствии посторонних (нереагирующих) веществ (M = A) выражение (3.5) превращается в:
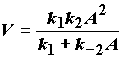 (3.6)
(3.6)
Выражение (3.6) объясняет наблюдаемый в эксперименте переход при уменьшении давления (концентрации А) от кинетических кривых первого порядка к кинетическим кривым второго порядка.
Схема Линдемана при качественно правильных предсказаниях кинетических закономерностей не подтверждается экспериментом количественно. Исследование зависимости константы первого порядка от давления инертного газа дает кривую, показанную на Рис. 3.1.
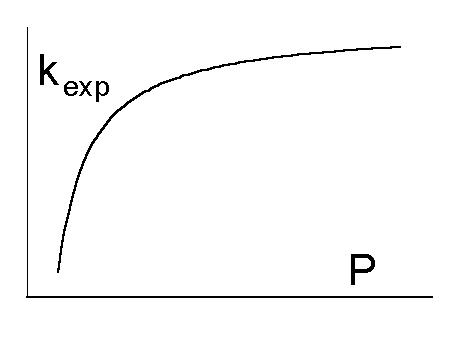
Модель, однако, предсказывает отклонение от постоянной константы скорости первого порядка при более высоких давлениях, чем это происходит в эксперименте. Кроме того, предсказываемая моделью линейная зависимость, получаемая из формулы (3.5):
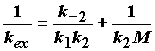
не подтверждается в эксперименте.
Более строгое рассмотрение кинетики мономолекулярной реакции сделано в теории Райса-Рамспергера-Касселя-Маркуса (РРКМ). В этой теории учтено, что колебательные состояния реагирующей молекулы квантованы. При столкновении может происходить переход молекулы из имеющегося колебательного состояния в любое другое. Скорость как самой реакции, так и процесса дезактивации активированной молекулы A* зависит от того, в котором колебательном состоянии находится молекула, т.е. k1 и k2 зависят от колебательной энергии молекулы E. Для подансамбля активированных молекул с данной энергией E константа скорости реакции k1(E) рассчитывается в соответствии с теорией переходного состояния. Таким образом, экспериментальная скорость реакции будет складываться из скоростей реакций для различных подансамблей:
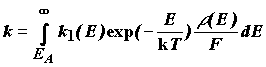 (3.7)
(3.7)
где ![]() (E) -
плотность распределения состояний по энергии,
т.е. число состояний в интервале энергий от E
до E+dE, F - сумма по состояниям.
(E) -
плотность распределения состояний по энергии,
т.е. число состояний в интервале энергий от E
до E+dE, F - сумма по состояниям.
Точное выражение для константы скорости реакции в теории РРКМ вместе с выводом можно найти в (1,2). Здесь необходимо отметить лишь то, что эта теория в явном виде учитывает время релаксации, которое соответствует передаче энергии от одной молекулы к другой в ходе столкновения. При этом считается, что время релаксации энергии по внутренним степеням свободы в молекуле очень мало (свободный обмен энергией между нормальными колебаниями). Вследствие разницы этих времен все активированные молекулы с данной энергией одинаковы и к ним применима теория переходного состояния.
3.4 Модель Крамерса
Другой метод явного учета процесса обмена энергией между реакционным комплексом и средой используется в модели Крамерса. Представим себе реакцию достаточно крупной молекулы в вязкой жидкости. Движение по координате реакции фрагментов молекулы со значительными массами не может быть очень быстрым. Молекулы растворителя, окружающие реакционный комплекс, находятся все время в контакте с ним и, таким образом, время релаксации, т.е. время обмена энергией со средой, мало. Реакционная система в жидкости характеризуется еще большим числом степеней свободы, чем реакционная система в газе. К внутренним степеням свободы молекулы необходимо прибавить степени свободы, характеризующие положение, ориентацию и колебания молекул среды, находящихся в контакте с реакционным комплексом. Выделим тем не менее степень свободы, отвечающую координате реакции. Остальные степени свободы будем рассматривать как тепловой резервуар, который находится в равновесии с реакционной степенью свободы. Появление на реакционной степени свободы необходимой энергии будем рассматривать как возникновение флуктуации. Крамерс предложил применить к движению изображающей точки по координате реакции формализм, предложенный для описания броуновской диффузии частицы в вязкой среде. Этот процесс описывается уравнением Ланжевена:
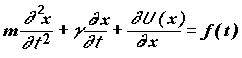 (3.8)
(3.8)
где x - координата реакции, m -
приведенная масса системы, ![]() - коэффициент трения, U -
потенциал, f(t) - случайная сила.
- коэффициент трения, U -
потенциал, f(t) - случайная сила.
Это уравнение следует из второго закона
Ньютона. Действительно, первый член уравнения -
ускорение частицы массой m. Второй член
уравнения - это сила трения, которая
пропорциональна скорости движения с
коэффициентом пропорциональности ![]() (коэффициент трения).
Третий член уравнения (градиент потенциала)
представляет собой силу, действующую на частицу
вследствие того, что она находится в потенциале.
(коэффициент трения).
Третий член уравнения (градиент потенциала)
представляет собой силу, действующую на частицу
вследствие того, что она находится в потенциале.
Если левую часть этого уравнения приравнять нулю, полученное выражение будет описывать затухающее движение в вязкой среде. Например, если потенциал параболический (для маятника, погруженного в жидкость), то движение будет периодическим затухающим колебанием. При любых начальных условиях такое движение очень быстро прекращается и достигается стационарное состояние системы. Ясно, что этот случай не может описать броуновскую диффузию, т.е. стохастический флуктуационный процесс, который никогда не останавливается. В связи с этим, в уравнение введена случайная сила f(t). Величина силы различна в различные моменты времени. Такая функция задается следующим образом:
<f(t)>=0
<f(t)f(t+![]() 1)>=
1)>=![]() (
(![]() 1)
1)
<f(t)f(t+![]() 1)f(t+
1)f(t+![]() 2)>=
2)>= ![]() (
(![]() 1,
1, ![]() 2)
2)
. . . . . . . . . . . . . . . .
Первая строка здесь указывает на то, что
среднее значение функции за большой промежуток
времени стремится к нулю. Во второй и далее
строчках приведены корреляторы (моменты)
случайной функции. В частности, вторая строчка
указывает, что вероятность найти величину
случайной силы одинаковой в момент времени t и в
момент времени t+![]() 1
равна
1
равна ![]() (
(![]() 1). Обычно
в численных расчетах используется нормально
распределенная случайная сила, т.е.
распределение величины случайной силы во
времени описывается гауссовой функцией. В этом
случае для полного ее задания достаточно указать
два коррелятора. Для правильного понимания
уравнения Ланжевена необходимо отметить, что для
случайной силы справедлива
флуктуационно-диссипативная теорема. Она
утверждает, что для некоррелированной случайной
силы
1). Обычно
в численных расчетах используется нормально
распределенная случайная сила, т.е.
распределение величины случайной силы во
времени описывается гауссовой функцией. В этом
случае для полного ее задания достаточно указать
два коррелятора. Для правильного понимания
уравнения Ланжевена необходимо отметить, что для
случайной силы справедлива
флуктуационно-диссипативная теорема. Она
утверждает, что для некоррелированной случайной
силы
<f(0)f(![]() )>=kT
)>=kT
![]()
![]() (
(![]() ) (3.9)
) (3.9)
где T - температура, ![]() - дельта-функция Дирака,
- дельта-функция Дирака, ![]() - коэффициент трения.
Это выражение указывает на то, что сила является
не коррелированной, и, одновременно, показывает
связь между случайной силой и коэффициентом
трения. Таким образом, эти два параметра не
являются независимыми. Если мы задали один из
них, то другой уже точно определен. Физический
смысл этой связи заключается в том, что оба
параметра характеризуют силу взаимодействия
молекулы со средой (тепловым резервуаром). Это
взаимодействие приводит как к приобретению
частицей кинетической энергии за счет случайной
флуктуации (броуновского толчка), так и к потере
имеющейся кинетической энергии, т.е. замедлению
за счет трения.
- коэффициент трения.
Это выражение указывает на то, что сила является
не коррелированной, и, одновременно, показывает
связь между случайной силой и коэффициентом
трения. Таким образом, эти два параметра не
являются независимыми. Если мы задали один из
них, то другой уже точно определен. Физический
смысл этой связи заключается в том, что оба
параметра характеризуют силу взаимодействия
молекулы со средой (тепловым резервуаром). Это
взаимодействие приводит как к приобретению
частицей кинетической энергии за счет случайной
флуктуации (броуновского толчка), так и к потере
имеющейся кинетической энергии, т.е. замедлению
за счет трения.
Коэффициент трения ![]() , таким образом, является ключевой
величиной в модели Крамерса. Если учесть, что
коэффициент трения есть величина, обратно
пропорциональная подвижности молекулы U,
и воспользоваться соотношением Эйнштейна для
коэффициента диффузии:
, таким образом, является ключевой
величиной в модели Крамерса. Если учесть, что
коэффициент трения есть величина, обратно
пропорциональная подвижности молекулы U,
и воспользоваться соотношением Эйнштейна для
коэффициента диффузии:
![]()
где k есть постоянная Больцмана, T - температура,
становится понятным, что коэффициент трения ![]() в уравнениях (3.8) и (3.9)
обратно пропорционален коэффициенту диффузии D.
Именно величина коэффициента трения определяет,
насколько быстро устанавливается
максвелл-больцмановское распределение энергии
по степеням свободы, т.е. насколько быстро
протекают процессы релаксации.
в уравнениях (3.8) и (3.9)
обратно пропорционален коэффициенту диффузии D.
Именно величина коэффициента трения определяет,
насколько быстро устанавливается
максвелл-больцмановское распределение энергии
по степеням свободы, т.е. насколько быстро
протекают процессы релаксации.
Наличие случайной силы в уравнении (3.8) приводит к тому, что движение по координате реакции не остановится никогда, хотя оно не будет все время направлено в сторону продуктов реакции, а превратится в случайные блуждания. Реакция произойдет, если в ходе таких случайных блужданий изображающая точка достигнет вершины барьера. Обратный процесс, так же как в теории переходного состояния, в модели Крамерса не учитывается.
Рассмотрим качественно результаты, которые предсказывает уравнение (3.8). Ограничимся при этом малой областью вблизи вершины барьера. В теории переходного состояния, как мы помним, константа скорости реакции определяется следующим образом:
![]() (3.10)
(3.10)
где ![]() - равновесная
концентрация реакционных комплексов, имеющих
достаточную энергию, т.е. находящихся на вершине
барьера;
- равновесная
концентрация реакционных комплексов, имеющих
достаточную энергию, т.е. находящихся на вершине
барьера;
![]() - частота преодоления
барьера, равная частоте колебаний в потенциале,
который представляет собой перевернутый барьер.
- частота преодоления
барьера, равная частоте колебаний в потенциале,
который представляет собой перевернутый барьер.
Чтобы оценить константу скорости реакции в соответствии с моделью Крамерса, усредним сначала уравнение (3.8) по всем молекулам, находящимся вблизи точки перевала, учитывая свойство случайной силы <f(t)>=0. В качестве потенциала используем перевернутый параболический барьер:
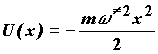 (3.11)
(3.11)
Получим уравнение:
![]() (3.12)
(3.12)
Решение характеристического уравнения:
![]()
даст частоту перехода W
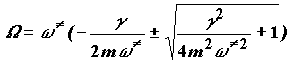 (3.13)
(3.13)
Рассмотрим предельные случаи этого решения.
1. Большое трение ![]() >>2m
>>2m![]()
В этом случае коэффициент трения в уравнении
Ланжевена достаточно велик, для установления
максвелл-больцмановского равновесия. Тогда
величина ![]() будет та же,
что в теории переходного состояния
будет та же,
что в теории переходного состояния ![]() .
.
Преобразуем скобку в решении (3.13) в виде:
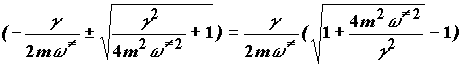
и используя малость 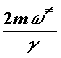 разложим квадратный корень в ряд, сохраняя два
первых члена (
разложим квадратный корень в ряд, сохраняя два
первых члена (![]() ).
).
Получим для частоты перехода 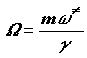
и для константы скорости 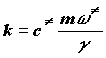
2. Среднее трение ![]() <
2m
<
2m![]()
Это условие означает, что трение, т.е. связь с
тепловым резервуаром, недостаточно велика, чтобы
воздействовать на систему в то время, пока она
находится в области седловой точки. Будем
считать, однако, что коэффициент трения
достаточно велик, чтобы поддерживать
максвелл-больцмановское распределение, т.е.
остается справедливым ![]() .
.
В этом случае можно пренебречь всеми членами в скобке (решение (3.13)) по сравнению с единицей.
![]()
Это означает, что частота перехода и константа скорости реакции совпадут с предсказаниями теории переходного состояния.
3. Теперь пусть коэффициент трения настолько
мал, что максвелл-больцмановское распределение
не успевает установиться. Это означает, что
величина ![]() меньше, чем
предсказывает теория переходного состояния.
меньше, чем
предсказывает теория переходного состояния.
Точное решение уравнения (3.8) дает зависимость константы скорости реакции от коэффициента трения, которая качественно показана на Рис. 3.2.
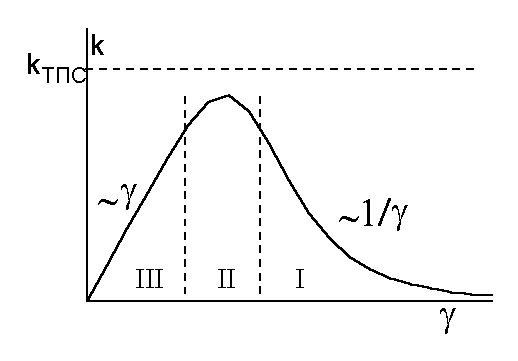
Можно разбить эту зависимость на три области. В области большого трения (I) константа скорости реакции обратно пропорциональна коэффициенту трения. Это означает, что среда настолько вязкая, что мешает продвижению изображающей точки по координате реакции. В таких условиях протекают реакции крупных частиц в вязких растворителях. В области среднего трения (II) константа скорости химической реакции в жидкости приближается к величине, предсказанной теорией переходного состояния для газа kтпс, однако не достигает этой величины. Это означает, что два приближения, лежащие в основе теории переходного состояния, в действительности не выполняются строго. В области малого трения (III) взаимодействие со средой недостаточно эффективно для поддержания равновесного распределения по энергии. Условия протекания реакции в этой области близки к тем, которые отражены в схеме Линдемана.
На Рис. 3.3. показано сравнение экспериментальных констант скорости изомеризации стильбена в возбужденном состоянии с предсказаниями модели Крамерса.
В качестве оси абсцисс на графике отложен обратный коэффициент диффузии, т.е. величина, пропорциональная коэффициенту трения.
При неплохом согласии с теорией обращает на
себя внимание более медленное по сравнению с
теорией убывание константы скорости с ростом
трения. Видно также, что левую ветвь кривой в этих
экспериментах надежно проверить не удалось. 
Это связано с тем, что в экспериментах в жидкой и газовой фазах при не слишком малых давлениях реализуются условия среднего и сильного трения.
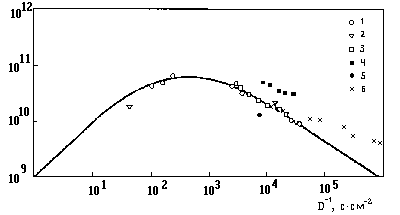
Рис.3.3. Корреляция между константой скорости
фотохимической изомеризации стильбена и
обратным коэффициентом диффузии в различных
средах при 298К.
1 - C2H6, 2 - C3H8, 3 - СО2, 4 -
Xe, 5 - SF6, 6 n-C6H14.
Кривая - расчет по модели Крамерса.
(Scroeder J.,Troe J.//Ann.Rev.Phys.Chem.,1987,v.38,p163.)
Модель Крамерса, предложенная в 1940 году, до настоящего времени продолжает привлекать внимание теоретиков. Уточнение модели происходит по двум основным направлениям. Оба направления связаны с попытками учета реального движения молекул среды, которое происходит в ходе элементарного акта реакции. В уравнении (3.8) влияние среды вводилось в виде коэффициента трения. Однако известно, что частица, движущаяся в жидкости, увлекает жидкость за собой - создается течение жидкости. Это течение затем влияет на движение породившей его частицы, поскольку оно имеет свою инерцию. Если принять во внимание этот фактор, то поведение системы в настоящий момент времени определяется уже не только параметрами системы в этот момент времени (действующими силами, энергией и т.п.), но и историей процесса, т.е. тем, какими были эти параметры в предыдущие моменты времени. В математике случайные процессы, независящие от предыстории, называются марковскими, а зависящие от нее - немарковскими. Учет немарковского фактора в теории броуновского движения макроскопических частиц приводит к обобщенному уравнению Ланжевена.
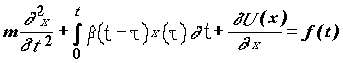 (3.14)
(3.14)
В этом уравнении вместо члена, содержащего
независящий от времени коэффициент трения,
введен интеграл, описывающий силу трения. Из
этого интеграла видно, что сила трения зависит не
только от того, какова скорость движения в данный
момент времени t, но и от того, какой она была в
предыдущие моменты времени (вплоть до t = 0, т.е.
момента создания системы). Насколько долго
система помнит свою историю (или насколько
быстро ее забывает)? описывает функция ![]() (t), которая
называется ядром трения. Для этого уравнения
также справедлива флуктуационно-диссипативная
теорема:
(t), которая
называется ядром трения. Для этого уравнения
также справедлива флуктуационно-диссипативная
теорема:
<f(0)f(![]() )>=kT
)>=kT![]() (
(![]() ) (3.15)
) (3.15)
Это выражение значительно более реалистично, чем приведенная выше формула (3.9). Действительно в (3.9) случайная сила абсолютно некоррелирована, т.е. длительность воздействия силы равна нулю. Этот идеализированный случай соответствует толчкам бесконечно малой длительности, но зато бесконечно большой величины. Реальные флуктуационные толчки, которые испытывает молекула, имеют конечную протяженность во времени и, таким образом, являются коррелированными.
Физический смысл памяти системы при использовании обобщенного уравнения Ланжевена для описания элементарного акта реакции заключается в инерции молекул растворителя, которые перемещаются синхронно с перемещениями молекулярных фрагментов по координате реакции. Решение такого уравнения в общем виде не получено. Поэтому его используют либо в каких-то приближениях для ограниченного диапазона условий, либо для решения задач молекулярной динамики в численном виде.
Другой способ уточнения модели Крамерса - рассмотрение координат, характеризующих молекулы среды, в явном виде. В этом случае ясно, что вместо одной координаты x, соответствующей координате реакции, мы должны записать уравнения движения по многим координатам, т.е. перейти к многомерной модели. Одномерная немарковская задача во многом эквивалентна многомерной марковской. Ограничимся качественным рассмотрением многомерной задачи Крамерса.
3.5 Многомерная модель Крамерса
Положение и ориентация молекул растворителя вокруг реакционного комплекса определяется набором координат qi. Расчеты структуры сольватного окружения различных молекул в настоящее время уже хорошо известны. Эти расчеты проводят добавляя к индивидуальной молекуле одну молекулу растворителя и выясняя минимум потенциальной энергии такой пары. Затем к паре можно добавить еще одну молекулу растворителя, снова определить минимум потенциальной поверхности и т.д. (Рис. 3.4).
Рис. 3.4. |
Рис.3.5 |
Результаты таких расчетов показали, что сольватационное окружение молекулы не имеет единственного минимума на поверхности потенциальной энергии. Поверхность потенциальной энергии с учетом молекул среды представляет собой целый ряд близко лежащих минимумов, разделенных небольшими энергетическими барьерами, высота которых сравнима с kT. Между этими минимумами происходят быстрые переходы, отвечающие изменениям конфигурации молекул растворителя вокруг реакционного комплекса. Нет никаких оснований выделить какой-либо из этих минимумов в качестве минимума реагентов. Сложность рельефа поверхности потенциальной энергии, очевидно, характерна не только для долины исходных реагентов, но и для области переходного состояния. Ясно, что единственная точка перевала, характерная для газовой фазы, заменяется множеством седловых точек, отмеченных крестиками на Рис. 3.5.
Расчет движения по столь сложной поверхности бесперспективен даже если бы удалось ее детально охарактеризовать. Поэтому в жидких растворах рассматривают поверхности, усредненные по большому ансамблю реакционных комплексов. При этом учитывается не только энергия каждой конфигурации, но и вероятность ее реализации. Такое усреднение эквивалентно переходу от поверхностей потенциальной энергии к поверхности свободной энергии. Такие поверхности по своему физическому смыслу значительно отличаются от ППЭ, которые мы рассматривали для газофазных реакций. В частности:
1. Координаты q i не являются нормальными координатами. Набор координат {qi} должен отражать:
- степень ориентированности диполей среды вокруг полярной молекулы;
- расстояния и ориентацию молекул, которые специфически взаимодействуют с реакционным комплексом, например, с образованием слабых водородных связей;
- упорядоченность молекул среды, которая может способствовать или препятствовать протеканию реакции, например, координационное число молекул среды, величину свободного объема в клетке, в которой происходит акт реакции и т.д.
2. Поскольку предполагается сильное взаимодействие рассматриваемой системы с тепловым резервуаром, эта система не является замкнутой, и с этой точки зрения поверхность свободной энергии не является адиабатическим термом. На этой поверхности нельзя, например, выделить колебательные уровни энергии.
3. Форму потенциальных ям, вообще говоря, можно аппроксимировать гармоническими потенциалами только вблизи точек равновесия (у дна ямы). Поскольку межмолекулярные взаимодействия характеризуются значительно меньшими энергиями, чем химические связи внутри молекулы, в форме поверхности проявляется очень сильный ангармонизм этих взаимодействий. В результате этого топология поверхности может быть достаточно сложной.
Ясно, что выделить определенные количественные характеристики, которые затем будут использоваться как координаты qi можно, только если в явном виде задать структуру и свойства молекулярного окружения реакционного комплекса. Чаще всего исследователи ограничиваются рассмотрением одной координаты растворителя q. В качестве такой координаты из интуитивных соображений выбирается то свойство растворителя, которое в наибольшей степени влияет на протекание реакции.
Рассмотрим качественно возможности многомерной модели. Выделим кроме координаты реакции еще одну координату q, которая будет характеризовать молекулы среды, окружающие реагирующий комплекс, в частности их положение и ориентацию. Тогда путь реакции можно представить себе как движение по двумерной поверхности свободной энергии из одного минимума в другой минимум, т.е. в двумерном двуямном потенциале (Рис.3.6). Взаимное расположение и форма потенциальных ям на этом рисунке могут быть различны. Для реакции изотопного обмена, например,
ROH+D2О ![]() ROD+HDO
ROD+HDO
в пренебрежении малыми различиями распределения заряда в молекулах с различным изотопным составом можно предполагать одинаковое сечение потенциальных ям исходного вещества и продукта реакции по координате растворителя q, т.е. поверхность является симметричной относительно оси, проходящей параллельно оси q через седловую точку (Рис. 3.6а).
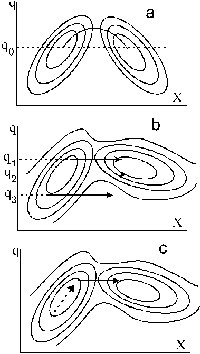
Для реакций, в ходе которых электронное распределение в исходных веществах и продуктах реакции различно, поверхность становится несимметричной (Рис. 3.6b). Отметим, что линии одинаковой энергии (изолинии) на рисунках совершенно не обязательно должны быть эллипсами.
Запишем два уравнения Ланжевена, описывающие движение по обеим координатам:
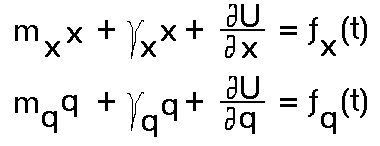 (3.16)
(3.16)
Вообще говоря, все параметры уравнений (3.16) -
эффективная массы, как мера инерции для движения,
случайная сила и связанная с ней величина
коэффициента трения, в этих двух уравнениях
различны. Качественное рассмотрение начнем со
случая бесконечно вязкой среды ![]() . Это приближение справедливо для
очень вязких растворов или стеклообразных
матриц. Оно предполагает, что реагирующий центр
не может за время эксперимента изменить величину
своей координаты q. Тогда частицы, с координатой q1
на Рис. 3.6b вступают в реакцию со своей константой
скорости и энергией активации. Протеканию
реакции соответствует изменение координаты x,
показанное на рисунке стрелкой. Частицы с
координатой растворителя q2 вступят в
реакцию с другой, меньшей константой скорости,
поскольку они преодолевают барьер не в седловой
точке. А частицы с координатой q3 вообще не
могут вступить в реакцию, поскольку без
изменения координаты растворителя такой переход
требует большой энергии. Кинетика реакции в этом
случае описывается суммой кинетических кривых
для частиц с разной координатой растворителя:
. Это приближение справедливо для
очень вязких растворов или стеклообразных
матриц. Оно предполагает, что реагирующий центр
не может за время эксперимента изменить величину
своей координаты q. Тогда частицы, с координатой q1
на Рис. 3.6b вступают в реакцию со своей константой
скорости и энергией активации. Протеканию
реакции соответствует изменение координаты x,
показанное на рисунке стрелкой. Частицы с
координатой растворителя q2 вступят в
реакцию с другой, меньшей константой скорости,
поскольку они преодолевают барьер не в седловой
точке. А частицы с координатой q3 вообще не
могут вступить в реакцию, поскольку без
изменения координаты растворителя такой переход
требует большой энергии. Кинетика реакции в этом
случае описывается суммой кинетических кривых
для частиц с разной координатой растворителя:
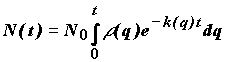
Такая кинетика носит название полиэкспоненциальной и часто наблюдается в случае реакций в твердой фазе.
Пусть теперь релаксация растворителя возможна,
т.е. координата q изменяется, однако ![]() .
.
В этом случае частицы с наиболее благоприятной сольватацией (в области точки перевала) быстро прореагируют. Далее реакция будет ограничиваться той скоростью, с которой частицы с неблагоприятной сольватацией продвигаются по поверхности свободной энергии в область благоприятной сольватации (Рис.3.6c). Это движение по механизму случайных блужданий описывается диффузионным уравнением по координате q. На кинетической кривой реакции можно выделить первую нестационарную фазу и затем стационарную часть кривой, которая будет описываться константой скорости такой диффузионно-контролируемой реакции. Очевидно, что величина этой константы скорости определяется характеристиками диффузии, т.е. перестройки среды, и не зависит от характеристик (например, энергии активации) собственно химического процесса.
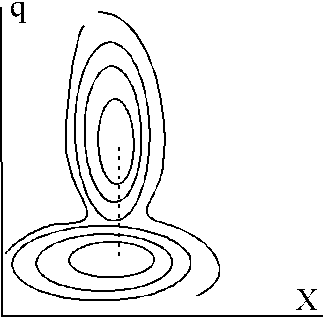
В качестве третьего примера многообразных типов кинетического поведения, которое предсказывается многомерной моделью Крамерса, приведем случай, при котором химическая реакция не требует существенной перестройки внутренних координат в реакционном комплексе, но требует существенной перестройки среды (Рис.3.7).
В этом случае энергетические минимумы, соответствующие исходным веществам и продуктам реакции, расположены на одной прямой, параллельной оси q. Такая ситуация характерна, например, для реакций внешнесферного переноса электрона. Здесь координата среды является единственной существенной координатой и движение по ней определяет скорость реакции.
3.6 Задачи
1. Приведите примеры неравновесных систем, укажите температуры различных подсистем. (Лазеры, металлы, плазма, ЭПР, ЯМР).
2. Предскажите качественный вид кинетических кривых, соответствующих Рис. 3.6b и 3.6c.
3. Оцените по порядку величины коэффициент диффузии, при котором начинается область сильного трения.
Оцените по порядку величины давление в области Линдемана. Объясните, почему в эксперименте отклонения от кинетического закона первого порядка происходят при более низких давлениях, чем это предсказывает схема Линедемана.
Литература.