Лекция 4. Реакции электронного переноса. Теория Маркуса.
4.1 Реакции переноса электрона
Перенос электрона с одной молекулы или иона на другую молекулу или ион является одной из самых распространенных элементарных реакций. Такая стадия обязательно присутствует в схемах окислительно-восстановительных процессов, электрохимических реакций, биохимических реакций фотосинтеза, дыхания и т.п. Большинство таких реакций, интересующих исследователей, протекает в жидких растворах. В реакции переноса электрона обязательно участвуют два фрагмента - донор электрона D (восстановительный реагент) и акцептор электрона A (окислительный реагент). Естественно, что для экспериментального изучения элементарной реакции переноса электрона выбираются наиболее простые модельные объекты, в которых эта реакция не осложняется перестройкой структуры молекулы, т.е. разрывом и образованием химических связей. В большом числе исследований в качестве таких модельных объектов были использованы ионы переходных металлов и их комплексные соединения. Различают два различных типа реакций переноса электрона. Если донорный и акцепторный фрагменты объединены в одну молекулу и находятся вблизи друг друга, то говорят о внутрисферной реакции переноса электрона. При этом предполагают, что волновые функции орбиталей, с которой уходит электрон и на которую он приходит, сильно перекрываются. Внутрисферными реакциями являются, в частности, реакции окисления или восстановления центрального иона в комплексном соединении лигандом, т.е. реакция переноса электрона с иона на лиганд или наоборот. Такие реакции часто наблюдаются в возбужденном состоянии молекул, которые получаются при поглощении ими кванта света.
Внешнесферной называется реакция переноса
электрона в паре частиц, каждая из которых может
существовать отдельно. В ходе внешнесферной
реакции частицы реагентов остаются химически
индивидуальными и находятся каждая в своем
сольватном или лигандном окружении. В качестве
примера приведем реакцию: [Fe(CN)6]3- + Cu+ ![]() [Fe(CN)6]4- + Cu2+ .
[Fe(CN)6]4- + Cu2+ .
Попробуем рассмотреть элементарный процесс переноса электрона в тех же приближениях, в которых мы рассматривали элементарную реакцию обмена. В соответствии с приближением Борна-Оппенгеймера, распределение электронов в молекуле находится в равновесии с ядерной конфигурацией. Перемещение электронной плотности с донора на акцептор должно определяться изменением каких-либо ядерных координат - смещением атомов или групп атомов. Для внутрисферных реакций можно представить себе изменение геометрии донорной и акцепторной частей молекулы, которое определяет скорость переноса электрона. Однако, простейшие модельные реакции внешнесферного переноса (например, приведенная выше) явно не связаны с большими перемещениями ядер. Таким образом, реакция переноса электрона, если она энергетически выгодна, должна протекать очень быстро и практически безактивационно. В эксперименте такое предсказание означает, что скорость реакции определяется частотой столкновений молекул донора и акцептора, т.е. реакция является диффузионно-контролируемой. Это предсказание не подтверждается экспериментом. Экспериментальные результаты можно суммировать следующим образом:
1. Даже экзоэргические реакции переноса
электрона являются активационными, т.е. даже если
свободная энергия реакции ![]() Gif < 0, энергия активации
Ea > 0.
Gif < 0, энергия активации
Ea > 0.
2. Выполняется правило Поляни-Семенова для энергии активации:
![]() Ea =
Ea = ![]()
![]() Gif + const.
Gif + const.
В применении к реакциям переноса электрона это
правило уточнено Бренстедом: ![]() = 1/2.
= 1/2.
3. Энергия активации зависит от диэлектрической
проницаемости (полярности) растворителя. С
ростом высокочастотной диэлектрической
проницаемости ![]()
![]() энергия активации
растет, с ростом низкочастотной диэлектрической
проницаемости
энергия активации
растет, с ростом низкочастотной диэлектрической
проницаемости ![]() 0
энергия активации падает.
0
энергия активации падает.
Напомним физический смысл величин ![]()
![]() и
и ![]() o .
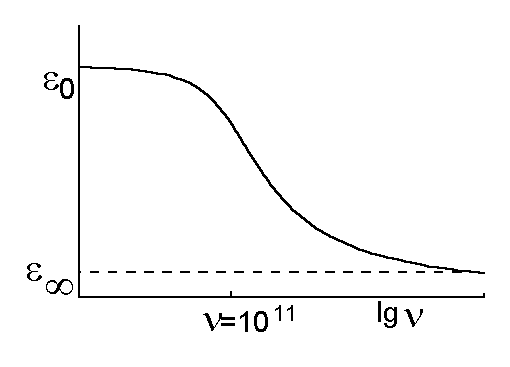
Экспериментально определенная величина
диэлектрической проницаемости зависит от
частоты электрического поля, которая
использовалась для определения (Рис. 4.1 ). При
низких частотах (в пределе при постоянном поле)
величина диэлектрической проницаемости
o .
Экспериментально определенная величина
диэлектрической проницаемости зависит от
частоты электрического поля, которая
использовалась для определения (Рис. 4.1 ). При
низких частотах (в пределе при постоянном поле)
величина диэлектрической проницаемости ![]() 0, значительно больше,
чем величина, получаемая при высоких частотах (
0, значительно больше,
чем величина, получаемая при высоких частотах (![]()
![]() при
при ![]()
![]()
![]() ). В частности, для
воды
). В частности, для
воды ![]()
![]() = 2, а
= 2, а ![]() o = 80.
Высокочастотная величина
o = 80.
Высокочастотная величина ![]()
![]() определяется электронной поляризацией молекул в
электрическом поле. Наиболее высокочастотным
электромагнитным воздействием на среду является
свет. В связи с этим
определяется электронной поляризацией молекул в
электрическом поле. Наиболее высокочастотным
электромагнитным воздействием на среду является
свет. В связи с этим ![]()
![]() =n2, где n -
коэффициент преломления света в среде.
Низкочастотная величина является суммарным
откликом от поляризации электронов в молекуле и
от ориентации диполей среды в электрическом
поле.
=n2, где n -
коэффициент преломления света в среде.
Низкочастотная величина является суммарным
откликом от поляризации электронов в молекуле и
от ориентации диполей среды в электрическом
поле.
Описанные выше экспериментальные закономерности для реакции переноса электрона не находили достаточно ясного и последовательного объяснения. Экспериментальный факт, который послужил толчком к созданию теории Маркуса, заключался в следующем. В ходе изучения реакции переноса электрона между ионами выяснилось, что энергия активации растет при уменьшении радиуса иона. Интуитивно представляется, что должна реализоваться противоположная зависимость. Таким образом, главная задача теории переноса электрона - объяснить природу энергетического барьера реакции.
4.2 Модель Маркуса
Модель Маркуса, предложенная в 1956 году, объясняет описанные выше экспериментальные факты с помощью следующих постулатов:
1. Ближняя координационная сфера реагирующих частиц не претерпевает изменений в ходе процесса переноса электрона. Таким образом, внутренние ядерные координаты реагирующих частиц вообще не рассматриваются, их изменение считается пренебрежимо малым.
2. Равновесие между исходными веществами в растворе и комплексом, состоящим из реагирующей пары донор/акцептор, считается установившимся. Это предположение означает, что мы исключаем из рассмотрения диффузионную стадию образования реакционной пары в клетке растворителя. Разделение продуктов реакции, т.е. их выход из клетки растворителя считается быстрым. Таким образом, рассматривается только кинетический режим протекания реакции в паре.
3. Источником возникновения энергии активации
является ориентационная поляризация среды - т.е.
молекул растворителя. Предполагается линейный
отклик среды, т.е. степень ориентационной
поляризации среды в каждой точке
пропорциональна напряженности электрического
поля в этой точке (~ ![]() E).
E).
В рамках этих постулатов дипольные молекулы среды, окружающие заряженную или дипольную реагирующую частицу, ориентированы. Каждая из молекул может быть охарактеризована зависимостью энергии от угла, который характеризует ее ориентацию. Эта зависимость в приближении линейной поляризации среды является параболической, т.е. молекулы среды находятся в гармоническом потенциале. Исходная пара донор/акцептор находится в своем равновесном поляризованном окружении, которое схематически показано на Рис.4.2.
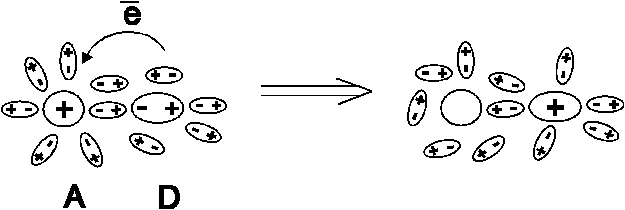
Продуктам реакции, т.е. той же самой паре, но с перенесенным электроном, соответствует другая равновесная ориентационная поляризация среды. Главная идея модели заключается в следующем. Совокупность молекул среды вблизи реагирующей пары частиц находится в непрерывном случайном движении. Для того, чтобы произошла реакция переноса электрона, необходимо, чтобы в ходе такого движения поляризация среды, соответствующая исходному состоянию, случайным образом нарушилась и сдвинулась в направлении поляризации, соответствующей продуктам реакции. Эта идея соответствует модели Крамерса с реакцией, полностью определяемой координатой растворителя, поверхность свободной энергии для которой схематически показана на Рис. 3.7.
4.3 Формула Маркуса
Рассмотрим подробнее сечение этой поверхности по координате среды (Рис. 4.3).
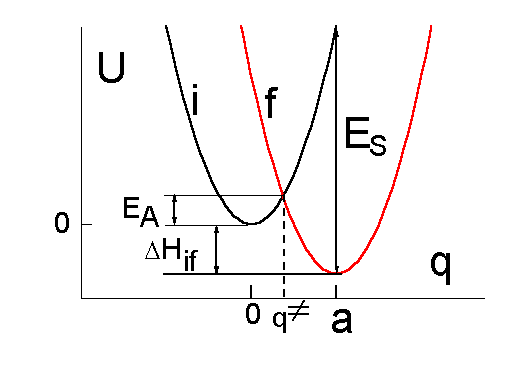
Профиль свободной энергии на этом рисунке возникает вследствие квазипересечения двух гармонических потенциалов, соответствующих ориентационной упорядоченности молекул среды вокруг исходного комплекса и вокруг продуктов реакции. Если система достигнет точки пересечения потенциалов, происходит мгновенный перенос электрона. Исходному состоянию соответствует гармонический потенциал с равновесным значением, которое мы примем за 0:
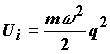 (4.1)
(4.1)
Потенциал для конечного состояния соответствует равновесной координате q = a
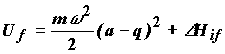
Этот потенциал сдвинут относительно исходного
на величину теплового эффекта реакции ![]()
В точке пересечения этих потенциалов Ui=Uf. Из этого условия получаем:
 (4.2)
(4.2)
где ![]() - координата
точки пересечения.
- координата
точки пересечения.
В этом выражении величина:
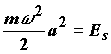 (4.3)
(4.3)
получила название энергии реорганизации среды. По физическому смыслу она представляет собой энергию, которую надо затратить, чтобы среда была "подстроена" под продукты реакции, но электрон остался в исходном состоянии (показана стрелкой на Рис. 4.3). Из соотношения (4.2) получается координата пересечения потенциалов:
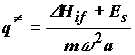
подставив которую в (4.1) получаем величину энергии активации:
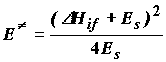 (4.4)
(4.4)
В этом простом выводе мы не учли, что поверхность свободной энергии многомерна, т.е. строится в зависимости от координат n молекул растворителя в непосредственной близости от реагирующего комплекса. С учетом этого потенциалы исходного и конечного состояний следует зависать в виде:
![]()
![]()
Выражение (4.4) при этом не изменяется.
Если дополнительно учесть, что различные
колебательные моды молекул растворителя
заселены с различной вероятностью, т.е. учесть
вырождение колебаний, то в выражениях для
энергий появляется энтропийный член. Таким
образом, в общем виде выражение (4.4) должно
связывать свободную энергию активации ![]() со свободной энергией
реакции
со свободной энергией
реакции ![]() :
:
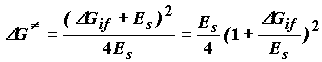 (4.5)
(4.5)
Эта формула носит название формулы Маркуса.
Предсказания величины энергии активации в соответствии с формулой (4.5) иллюстрируются следующим образом.
1. На Рис. 4.4а показан случай безбарьерного
переноса. Он соответствует пересечению
потенциалов вблизи дна потенциала продуктов
реакции. Этот случай характеризуется свободной
энергией активации![]() . В
эксперименте этот случай должен наблюдаться для
сильно эндоэргических реакций.
. В
эксперименте этот случай должен наблюдаться для
сильно эндоэргических реакций.
|
|
|
|
2. Увеличение энергии Гиббса реакции превращает случай безбарьерного переноса в обычный активационный процесс (Рис. 4.4b). В соответствии с формулой (4.5) выполняется правило Поляни-Семенова.
3. Для сильно экзоэргических реакций
пересечение поверхностей может лежать в области
дна потенциала исходных веществ (Рис. 4.4c). Этот
случай соответствует безактивационному
процессу ![]() . Очевидно, что
скорость безактивационной реакции
ограничивается скоростью столкновений
реагентов в ходе диффузии. Таким образом, этому
случаю соответствует диффузионная константа
скорости реакции. Обратим также внимание на то,
что безбарьерный и безактивационный перенос
электрона - это одна и та же ситуация с заменой
направления реакции.
. Очевидно, что
скорость безактивационной реакции
ограничивается скоростью столкновений
реагентов в ходе диффузии. Таким образом, этому
случаю соответствует диффузионная константа
скорости реакции. Обратим также внимание на то,
что безбарьерный и безактивационный перенос
электрона - это одна и та же ситуация с заменой
направления реакции.
4. На Рис. 4.4d пересечение поверхностей происходит на другой ветви потенциала исходных веществ. Несмотря на дальнейшее уменьшение свободной энергии реакции, снова появляется активационный барьер.
Все эти типы поведения содержатся в формуле Маркуса (4.5). В целом, модель Маркуса позволяет предсказать константу скорости реакции переноса электрона:
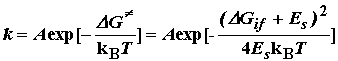 (4.6)
(4.6)
где kB - константа Больцмана, А - частотный фактор.
Зависимость константы скорости реакции от свободной энергии ведет себя, как показано на Рис.4.5.
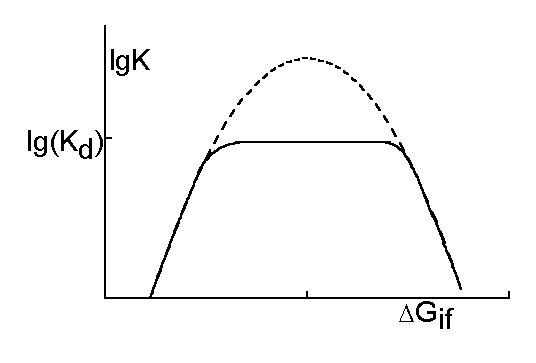
При увеличении энергетического эффекта реакции константа скорости реакции сначала растет, затем выходит на диффузионный предел, и затем опять падает в так называемой инвертированной области Маркуса, т.е. имеет колоколообразный характер.
4.4 Сравнение с экспериментом. Энергия реорганизации среды
В формуле Маркуса остается один неизвестный
параметр - величина энергии реорганизации среды
Es. Она может быть оценена из простых физических
соображений. Известно решение задачи Борна:
энергия непрерывной среды с диэлектрической
проницаемостью ![]() при внесении в нее заряда q заданного радиуса a
изменяется на величину:
при внесении в нее заряда q заданного радиуса a
изменяется на величину:
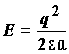 . (4.7)
. (4.7)
Поскольку интересующая нас энергия реорганизации включает в себя только ориентационную составляющую, из величины (4.7) нужно вычесть энергию, связанную с электронной поляризацией молекул. Тогда энергия реорганизации среды при внесении заряда в среду выражается формулой:
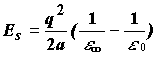 (4.8)
(4.8)
Для оценки энергии реорганизации в реакции переноса электрона необходимо учесть, что заряд вносится не из бесконечности, а переносится из одной точки пространства в другую. Как правило, молекулы донора и акцептора расположены достаточно близко, поэтому необходимо использовать так называемую модель проникающих сфер, которая учитывает, что сферы поляризации среды в исходном и конечном состояниях пересекаются. Эта модель приводит к следующей формуле:
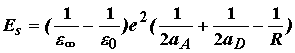 (4.9)
(4.9)
где e - заряд электрона, aA и aD - радиусы акцептора и донора, соответственно, R - расстояние между центрами.
Предложенная Маркусом модель интенсивно проверялась экспериментально. Особо пристальный интерес вызвало предсказание так называемой "инвертированной области Маркуса", в которой должно наблюдаться парадоксальное увеличение энергии активации и, соответственно, уменьшение скорости реакции переноса электрона при переходе к более энергетически выгодным процессам. На ряде систем экспериментально было подтверждено наличие такой области.
Наиболее удобными для экспериментальной проверки модели Маркуса оказались фотохимические реакции переноса электрона. Это связано с тем, что фотохимические эксперименты позволяют относительно легко изучать быстрые химические превращения. Действительно, в возбужденном состоянии, которое получается при поглощении молекулой фотона, существенно изменяются донорные и акцепторные свойства, т.е. способность молекулы принимать и отдавать электрон. Коротким импульсом света легко создать в растворе значительную концентрацию молекул в возбужденном состоянии, которые будут играть роль одного из партнеров реакции, например, акцептора электронов. Если в растворе находятся также молекулы другого партнера - донора электронов, то в ходе реакции переноса электрона молекулы акцептора в возбужденном состоянии исчезают и образуются ион-радикалы донора и акцептора, т.е. продукты реакции:
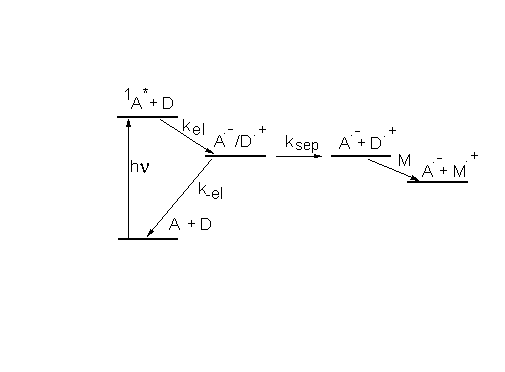
Схема на Рис.4.6. показывает:
- процесс поглощения света, который приводит к образованию синглетного возбужденного состояния 1A*;
- реакцию переноса электрона с константой скорости kel , которая приводит к образованию ион-радикальной пары в клетке растворителя;
- процесс диффузионного разделения образовавшихся ион-радикалов, т.е. их выхода из клетки растворителя с константой скорости ksep;
- конкурирующую с процессом диффузионного разделения обратную реакцию переноса электрона с константой скорости k-el. Эта реакция приводит к потере электронного возбуждения с образованием молекул исходных реагентов;
- реакцию переноса электрона между катион-радикалом донора и посторонней молекулой M.
За протеканием такой реакции переноса электрона можно следить, фиксируя количество ион-радикалов или время жизни исходного возбужденного состояния. В последнем случае реакция переноса электрона проявит себя как уменьшение времени жизни возбужденного состояния. Такое уменьшение времени жизни в фотохимии называется "тушением" возбужденного состояния.
Значительное число экспериментальных работ,
направленных на проверку модели Маркуса,
показало, что при качественном согласии с
экспериментом, количественные измерения дают
существенные расхождения с формулами (4.5) и (4.6). В
связи с этим в настоящее время разрабатывается
целый спектр моделей, которые усовершенствуют и
уточняют модель Маркуса. Такие
усовершенствования учитывают вклад
реорганизации внутренней сферы в энергию
активации реакции. Действительно, даже в
комплексных ионах переходных металлов изменение
заряда иона должно привести к изменению длин
связей иона с лигандами, изменению частот
колебаний и т.д. Для более сложных молекул
необходимо рассматривать координаты среды и
внутренние химические координаты как
равноправные. В таком случае в формулах (4.5) и (4.6)
вместо энергии реорганизации среды ![]() необходимо использовать суммарную
энергию
необходимо использовать суммарную
энергию ![]() :
:
![]()
где Es - энергия реорганизации среды, а Ei энергия реорганизации внутренних координат.
Для количественного сравнения эксперимента с теорией необходимо также уточнить предэкспоненциальный фактор в формуле (4.6), который должен учесть вероятность и скорость перехода системы с терма исходного состояния на терм продуктов реакции в области их квазипересечения. Если считать, что адиабатическое расщепление характеризуется матричным элементом V, то константа скорости реакции в одном из вариантов теории записывается как:
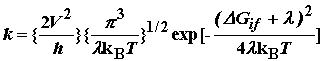 (4.10)
(4.10)
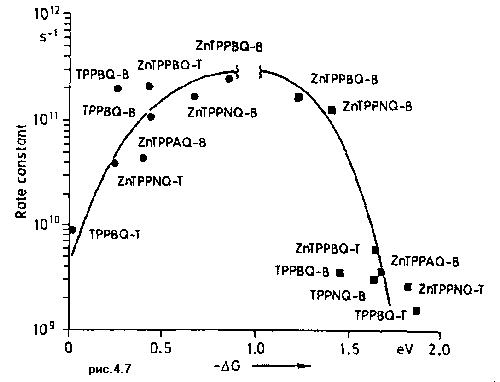
Развитие и уточнение модели Маркуса позволяет для конкретных систем получать формулы, хорошо описывающие результаты эксперимента. Например, на Рис.4.7. показана зависимость константы скорости для реакций
1P* + Q ![]() P+ +Q-
P+ +Q-
P+ +Q- ![]() P + Q
P + Q
где P и Q - производные порфирина и хинона, от свободной энергии реакции. Донор и акцептор в этом случае были связаны между собой химическими мостиками, так что диффузионная стадия сближения реагентов отсутствовала. В результате измеренная константа скорости превышает диффузионный предел, и предсказываемая теорией зависимость может быть проверена более надежно. Рис 4.7. демонстрирует хорошее согласие теории с результатами эксперимента как в обычной, так и в инвертированной области Маркуса.
4.5 Задачи
1. Рассчитайте энергию реорганизации среды для процесса электрохимического восстановления иона Cu2+ с образованием Cu+ в воде, спирте и ацетонитриле.
2. Рассчитайте энергию активации для реакции переноса электрона между ферроцианид-ионом [Fe(CN)6]4- и феррицианид-ионом [Fe(CN)6]3-).
3. Оцените, при каком ![]() G реакции будет наблюдаться диффузионный
предел при реакции переноса электрона между
двумя ароматическими соединениями в водном и в
углеводородном растворе.
G реакции будет наблюдаться диффузионный
предел при реакции переноса электрона между
двумя ароматическими соединениями в водном и в
углеводородном растворе.
Литература.
1.М.В.Базилевский, В.И.Фаустов. Современные теории
химических реакций в конденсированной фазе.
Успехи химии. 1992, т.61, N. 7, с.1185-1223.