Лекция 5. Туннельные эффекты в химии
5.1 Экспериментальное наблюдение туннельного
эффекта.
До сих пор рассмотрение элементарных химических реакций мы проводили в полуклассическом приближении. Рассматривая изменение электронных волновых функций в ходе реакции, мы использовали уравнение Шредингера, т.е. квантово-механический подход. В то же время движение по поверхности потенциальной энергии рассматривалось как движение, протекающее по законам классической механики. Между тем атомы и группы атомов представляют собой микрообъекты, движение которых, вообще говоря, также надо рассматривать с точки зрения квантовой механики. Явления, которые предсказывает квантовая механика, многообразны. Однако в экспериментальной химической кинетике они проявляются довольно редко. Одним из наиболее ярких проявлений в эксперименте квантовых эффектов является процесс туннелирования.

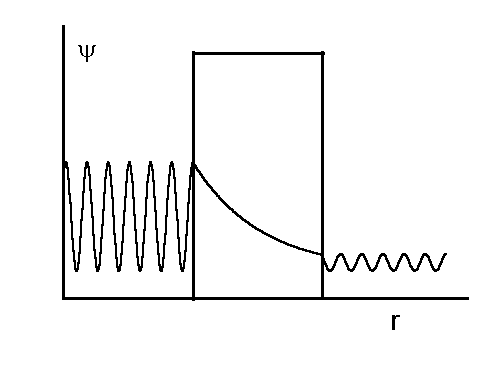
Напомним объяснение туннельного эффекта. Если рассматривается микрообъект, например, электрон в потенциальной яме, то в отличие от классической механики существует конечная вероятность обнаружить этот объект в запрещенной области пространства, там, где его полная энергия меньше, чем потенциальная энергия в этой точке. Вероятность нахождения электрона описывается квадратом волновой функции. На Рис.5.1 видно, что волновая функция электрона экспоненциально спадает внутри потенциального барьера.
Таким образом, если ширина и высота барьера не слишком велики, существует вероятность найти электрон за пределами потенциальной ямы, за барьером, преодолеть который с классической точки зрения он не может. Для химии наиболее интересным является туннелирование более тяжелых объектов - атомов и групп атомов. Одним из первых экспериментальную проверку эффектов туннелирования на примере реакций переноса протона (кислотно-основных реакций) предпринял Р.Белл. В нашей стране экспериментальное и теоретическое рассмотрение процессов туннелирования в химии связано с именем В.И.Гольданского.
Экспериментально процессы туннелирования
регистрируются в основном двумя методами.
Кинетический метод основан на регистрации
перехода между двумя состояниями молекулярной
системы, разделенными энергетическим барьером.
Если в условиях эксперимента энергетический
барьер между состояниями столь высок, что
активационный, надбарьерный переход между ними
невозможен, то экспериментальное наблюдение
перехода свидетельствует о туннельном механизме
процесса. Спектроскопический подход к
экспериментальному изучению туннельных
процессов основан на эффекте туннельного
расщепления энергетических уровней. Качественно
эффект расщепления можно объяснить следующим
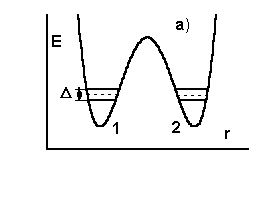
образом. Рассмотрим молекулярную систему, два
состояния которой разделены энергетическим
барьером (Рис.5.2а). Каждому из состояний
соответствует своя волновая функция ![]() 1 и
1 и ![]() 2, и
соответствующие уровни энергии Е1 и Е2. Процесс
туннелирования между этими двумя состояниями
предполагает, что амплитуда волновой функции
2, и
соответствующие уровни энергии Е1 и Е2. Процесс
туннелирования между этими двумя состояниями
предполагает, что амплитуда волновой функции ![]() 1 в
области состояния 2 не равна нулю и наоборот.
Таким образом, волновые функции двух состояний в
некоторой степени перекрываются. Такое
перекрывание, как мы знаем, вызывает их
смешивание и образование двух новых волновых
функций с другими уровнями энергии, т.е.
расщепление энергетических уровней, качественно
показанное на Рис.5.2b. Величина такого
туннельного расщепления, обозначенного на
Рис.5.2а величиной
1 в
области состояния 2 не равна нулю и наоборот.
Таким образом, волновые функции двух состояний в
некоторой степени перекрываются. Такое
перекрывание, как мы знаем, вызывает их
смешивание и образование двух новых волновых
функций с другими уровнями энергии, т.е.
расщепление энергетических уровней, качественно
показанное на Рис.5.2b. Величина такого
туннельного расщепления, обозначенного на
Рис.5.2а величиной ![]() ,
зависит от величины перекрывания волновых
функций и, следовательно, характеризует частоту
туннельного перехода между состояниями. В
эксперименте туннельное расщепление
проявляется как расщеплении полос поглощения и
флуоресценции молекул в инфракрасном, видимом и
ультрафиолетовом спектральных диапазонах.
Экспериментально зафиксированы величины
туннельного расщепления, лежащие в диапазоне от
долей до нескольких сотен см-1. Очевидно,
что такие расщепления означают протекание
туннельных переходов с достаточно высокой
частотой. Это переходы, требующие небольших
смещений легких частиц - превращения между
таутомерами и изомерами близкой структуры,
вращения молекулярных фрагментов и т.п. Такие
туннельные процессы изучаются
спектроскопическими методами. Химические
реакции требуют, как правило, перемещений
больших молекулярных фрагментов, которые не
могут туннелировать с большой частотой. Поэтому
туннельные химические реакции изучаются
кинетическим методом, наблюдая кинетику
перехода системы из одного состояния в другое.
,
зависит от величины перекрывания волновых
функций и, следовательно, характеризует частоту
туннельного перехода между состояниями. В
эксперименте туннельное расщепление
проявляется как расщеплении полос поглощения и
флуоресценции молекул в инфракрасном, видимом и
ультрафиолетовом спектральных диапазонах.
Экспериментально зафиксированы величины
туннельного расщепления, лежащие в диапазоне от
долей до нескольких сотен см-1. Очевидно,
что такие расщепления означают протекание
туннельных переходов с достаточно высокой
частотой. Это переходы, требующие небольших
смещений легких частиц - превращения между
таутомерами и изомерами близкой структуры,
вращения молекулярных фрагментов и т.п. Такие
туннельные процессы изучаются
спектроскопическими методами. Химические
реакции требуют, как правило, перемещений
больших молекулярных фрагментов, которые не
могут туннелировать с большой частотой. Поэтому
туннельные химические реакции изучаются
кинетическим методом, наблюдая кинетику
перехода системы из одного состояния в другое.
Приведем примеры экспериментального наблюдения туннелирования в химии.
1. Одним из наиболее широко известных примеров туннельного процесса является инверсия аммиака (Рис. 5.3.).
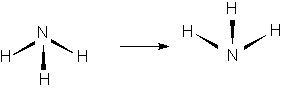
В этом процессе молекула аммиака
выворачивается подобно зонтику на ветру. Процесс
инверсии проявляется в эксперименте как
расщепление полосы поглощения зонтичного
колебания в ИК-спектрах. Высота потенциального
барьера, разделяющего две стационарных
состояния, составляет Vo = 24,83 кДж/моль. Частота
туннельного перехода ~ 2.108 с-1 при туннелирующей
массе ~ 2,54 а.е.м. и эффективной длине - 0,77 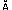 . Обратим внимание на то, что туннелирующая масса
значительно меньше массы трех атомов водорода.
Это означает, что в процессе туннелирования
происходит согласованное движение всех атомов,
включая азот, т.е. движение по нормальной
координате. Частота туннелирования значительно
падает, если произвести дейтерирование молекулы
аммиака.
. Обратим внимание на то, что туннелирующая масса
значительно меньше массы трех атомов водорода.
Это означает, что в процессе туннелирования
происходит согласованное движение всех атомов,
включая азот, т.е. движение по нормальной
координате. Частота туннелирования значительно
падает, если произвести дейтерирование молекулы
аммиака.
2. Другим хорошо изученным туннельным процессов является внутримолекулярный туннельный перенос атома водорода в малоновом альдегиде в его енольной форме (Рис.5.4). Этот процесс в основном колебательном состоянии молекулы вызывает туннельное расщепление величиной 21,6 см-1, которое проявляется в микроволновых спектрах поглощения. При дейтерировании молекулы величина расщепления уменьшается до 3 см-1.
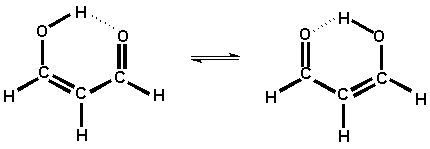
Отметим, что перенос атома водорода в молекуле малонового альдегида сопровождается изменением длин С-С и С-О связей, поскольку меняется порядок этих связей. Таким образом, этот пример также показывает, что туннельная реакция является коллективным движением многих частиц.
3. Примером туннельного протекания химической реакции является процесс полимеризации формальдегида при гелиевых температурах:
H(OCH2)n+ + OCH2 ![]() H(OCH2)n OCH2+
(5.1)
H(OCH2)n OCH2+
(5.1)
Эта цепная реакция инициируется реакцией
переноса протона на молекулу формальдегида с
молекулы кислоты. В реальном эксперименте в
качестве кислоты выступают катион-радикалы,
получаемые при ![]() -облучении,
или возбужденные состояния, получаемые при
фотовозбуждении (например, при фотовозбуждении
нитрофенола). Константа скорости присоединения
мономерного звена к полимерной цепи может быть
измерена с помощью регистрации ИК-спектров
пленки формальдегида, напыленной на охлаждаемую
поверхность. Оказалось, что величина константы
скорости k=1,6x102 с-1 не зависит от температуры
в интервале 4,2 - 12К. Если бы реакция
подчинялась закону Аррениуса, то при гелиевых
температурах среднее время присоединения звена
составило бы
-облучении,
или возбужденные состояния, получаемые при
фотовозбуждении (например, при фотовозбуждении
нитрофенола). Константа скорости присоединения
мономерного звена к полимерной цепи может быть
измерена с помощью регистрации ИК-спектров
пленки формальдегида, напыленной на охлаждаемую
поверхность. Оказалось, что величина константы
скорости k=1,6x102 с-1 не зависит от температуры
в интервале 4,2 - 12К. Если бы реакция
подчинялась закону Аррениуса, то при гелиевых
температурах среднее время присоединения звена
составило бы ![]() o=10100
лет.
o=10100
лет.
4. Туннельным образом может протекать реакция
отрыва атома водорода типа: CH3. + CH3OH
![]() CH4 + .СH2OH
(5.2)
CH4 + .СH2OH
(5.2)
Так же, как и в других примерах, реакция отрыва атома водорода протекает практически классическим, надбарьерным способом в области обычных температур, но в твердых матрицах при низких температурах, когда надбарьерная траектория практически недостижима, наблюдается медленная реакция по туннельному механизму. При температуре 4,2К в стекле метанола эта реакция имеет характерное время 3х103 с.
5. Наиболее легкой частицей, принимающей участие в химических реакциях, является электрон. Перераспределение электронов внутри реакционного комплекса происходит очень быстро и обсуждение туннельного механизма их движения теряет смысл. Однако в условиях, когда донорная и акцепторная молекулы не могут сблизиться, наблюдается перенос электрона на большие расстояния. В работах К.И.Замараева показано, что в твердых матрицах при температуре жидкого азота (77К) и ниже наблюдается перенос электрона с донора на акцептор, расположенный на расстоянии 10-30 нм с характеристическим временами порядка минут и часов. Такие процессы также описываются как туннельные.
6. Туннелирование более тяжелых частиц, но на меньшие расстояния, предполагается во многих других случаях. В частности двуямная модель стеклообразного состояния вещества предполагает, что структурные фрагменты стекла находятся в потенциале, показанном на Рис.5.5. Двуямный потенциал возникает вследствие того, что структурные элементы в неупорядоченном твердом теле могут иметь два (а возможно и более) приблизительно одинаковых по энергии положения. В качестве иллюстрации на Рис. 5.5 приведены два положения кислородного мостка соединяющие атомы кремния в силикатном стекле. Переход из одного положения в другое при низких температурах может осуществляться только туннельным образом.
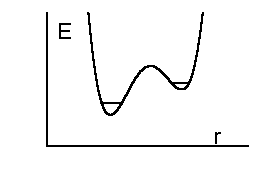
Эта модель была разработана для объяснения неклассических зависимостей теплоемкости, теплопроводности и других физических свойств большого набора различных стекол при гелиевых температурах. Поскольку переход из одного стационарного состояния потенциала в другое требует энергии (потенциал не симметричен), предполагаются фононно-стимулированные туннельные переходы, т.е. переходы, которые происходят с одновременным поглощением или испусканием колебательного кванта - фонона.
Приведенные примеры показывают, что туннельные процессы в явном и ярком виде наблюдаются в эксперименте при низких, чаще всего гелиевых, температурах. Это, однако, не означает, что туннельные процессы не происходят при более высоких температурах. В обычных условиях значительно труднее отделить квантовые эффекты от движений по классическим траекториям, которые происходят одновременно. Поэтому при высоких температурах туннельные явления описываются как поправки к классическому рассмотрению.
5.2 Низкотемпературный предел скорости реакции
Рассмотрим простейший теоретический подход для описания реакций, протекающих по туннельному механизму. На Рис.5.6 показан потенциальный барьер на пути реакции с координатой Q.
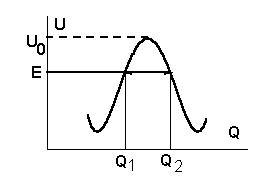
Учтем, что в долине исходных веществ существует распределение Максвелла-Больцмана. Для частицы с любой энергией существует конечная вероятность туннельного преодоления барьера w(E). Поскольку ширина барьера на разной высоте различна, эта вероятность зависит от энергии частицы. Тогда константа скорости реакции будет определяться суммой вероятностей прореагировать для каждой частицы:
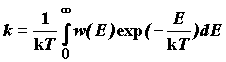 (5.3)
(5.3)
Для вычисления вероятности туннелирования воспользуемся формулой Гамова для вероятности туннелирования частицы через барьер с координатами начала и конца подбарьерной траектории a и b:
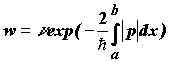 (5.4)
(5.4)
Здесь n - частота колебаний частицы в потенциальной яме, p - импульс частицы внутри барьера. Импульс взят по модулю, поскольку кинетическая энергия частицы внутри барьера отрицательна и импульс является мнимой величиной. Отметим, что в этой формуле содержится информация не только о ширине барьера, но и о его высоте. Действительно, в выражении для импульса:
![]()
входит высота и форма барьера. Там же видна зависимость вероятности туннелирования от массы частицы.
В рассматриваемом случае пределы интегрирования в формуле (5.4) зависят от энергии частицы. На Рис.5.6 они обозначены как Q1(E) и Q2(E). Обозначим интеграл в формуле (5.4) как S(E):
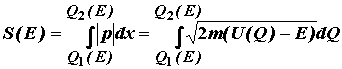 (5.5)
(5.5)
Тогда выражение для константы скорости реакции примет вид:
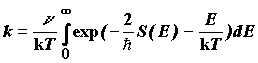 (5.6)
(5.6)
Это выражение должно описывать не только туннельную реакцию, но и надбарьерные, классические траектории. Оно учитывает два квантовых эффекта - туннельное прохождение барьера и надбарьерное отражение. Квантовый эффект надбарьерного отражения заключается в том, что даже если частица имеет кинетическую энергию, превышающую потенциальный барьер, вероятность преодоления барьера не равна единице. Существует конечная вероятность отражения такой частицы обратно.
В соответствии с формулой (5.6) частицы с любой
энергией вносят вклад в константу скорости
реакции. Однако этот вклад различен. Он
определяется произведением числа частиц с
данной энергией E* и вероятности преодоления
барьера для них. При высоких температурах число
частиц с энергией, превышающей высоту барьера,
велико, вероятность преодолеть барьер для них
также велика, и, таким образом, они вносят
основной вклад в скорость реакции. Это случай
классического надбарьерного протекания реакции.
При понижении температуры энергия частиц
уменьшается. В пределе при T ![]() 0 все частицы имеют энергию нулевых
колебаний, т.е. находятся вблизи дна
потенциальной ямы. Реакция в этом случае
протекает только туннельным образом,
преодолевая барьер в его самой широкой части. При
промежуточных температурах в константу скорости
реакции будет вносить основной вклад группа
частиц с энергией E*, для которых произведение
равновесной заселенности на вероятность
перехода максимально. Именно эта энергия E* будет
наблюдаться в эксперименте как эффективная
энергия активации при данной температуре. Найдем
эту величину из условия максимума
подынтегрального выражения в формуле (5.6). Это
условие эквивалентно условию минимума
показателя степени в экспоненте, которое мы
найдем, продифференцировав показатель степени
по энергии и приравняв его нулю:
0 все частицы имеют энергию нулевых
колебаний, т.е. находятся вблизи дна
потенциальной ямы. Реакция в этом случае
протекает только туннельным образом,
преодолевая барьер в его самой широкой части. При
промежуточных температурах в константу скорости
реакции будет вносить основной вклад группа
частиц с энергией E*, для которых произведение
равновесной заселенности на вероятность
перехода максимально. Именно эта энергия E* будет
наблюдаться в эксперименте как эффективная
энергия активации при данной температуре. Найдем
эту величину из условия максимума
подынтегрального выражения в формуле (5.6). Это
условие эквивалентно условию минимума
показателя степени в экспоненте, которое мы
найдем, продифференцировав показатель степени
по энергии и приравняв его нулю:
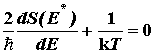
Подставив выражение (5.5) получим:
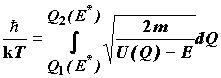 (5.7)
(5.7)
Из этого уравнения может быть найдена величина E*. Видно, что
при T ![]()
![]() E* = U0;
E* = U0;
при T ![]() 0 E* = 0;
0 E* = 0;
В целом зависимость экспериментальной энергии активации, в соответствии с этой формулой, должна качественно выглядеть, как показано на Рис.5.7.
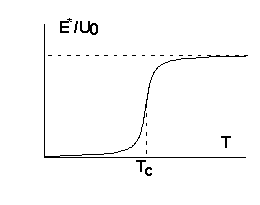
На этой зависимости можно выделить область температур, в которой энергия активации равна нулю, т.е. константа скорости реакции не зависит от температуры. Эта область носит название области низкотемпературного предела скорости химической реакции. С увеличением температуры наблюдаемая энергия активации должна плавно выйти на величину равную высоте преодолеваемого барьера. На Рис.5.7 показана величина Tc, которая называется критической температурой туннелирования. Она приблизительно указывает температуру, выше которой реакция протекает по классическому надбарьерному механизму, а ниже которой - туннельно. Эта критическая температура может быть оценена из формулы (5.7). Для этого в подынтегральном выражении надо в явном виде определить форму потенциального барьера. Такие расчеты были проведены для барьеров различной формы и дали следующий результат:
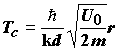 (5.8)
(5.8)
где d - ширина барьера, U0 -
его высота, m - масса туннелирующей
частицы, r - параметр, характеризующий
форму барьера. Для прямоугольного барьера r
= 1/2, для параболического барьера r = 2/![]() , для треугольного
барьера r = 3/4.
, для треугольного
барьера r = 3/4.
Таким образом, рассмотрение простой модели туннельного эффекта предсказывает, что скорость любой элементарной химической реакций при понижении температуры стремится не к нулю, а к некоторому низкотемпературному пределу. Для некоторых реакций предсказанное теорией поведение действительно наблюдается в эксперименте.
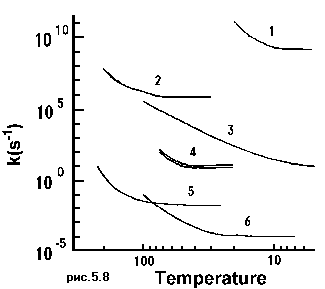
На Рис.5.8 показана температурная зависимость константы скорости следующих процессов:
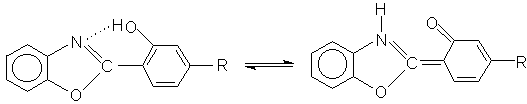
Cl. + H2C=CH2 ![]() H2ClC-CH2. (5.10)
H2ClC-CH2. (5.10)
H2ClC-CH2. +Cl2 ![]() H2ClC-CH2Cl +Cl.
H2ClC-CH2Cl +Cl.
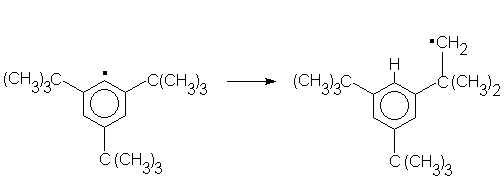
Из Рис.5.8. видно, что критическая температура для низкотемпературного предела скорости процесса обычно ниже 100К. Для большинства химических превращений низкотемпературный предел наблюдать вообще не удается. Это объясняется, во-первых, тем, что параметры, определяющие скорость туннельного превращения - масса, высота и ширина барьера, таковы, что скорость реакции на низкотемпературном пределе слишком мала для экспериментального наблюдения. Кроме того, низкотемпературное плато не является обязательным свойством туннельных реакций. Предсказание низкотемпературного предела скорости туннельной реакции мы получили в рамках крайне упрощенной модели. Для количественного предсказания скорости туннельных реакций и ее температурной зависимости необходимо учесть ряд дополнительных факторов. Перечислим некоторые наиболее важные из них.
1. Реакция рассматривалась нами как переход из потенциальной ямы в континуум, допускающий свободное движение. В действительности в конденсированной фазе реакция представляет собой переход из одной потенциальной ямы в другую. В каждой из этих ям существуют свои колебательные уровни энергии. Известно, что в случае резонансного расположения уровней энергии в потенциальных ямах исходного и конечного состояния вероятность туннельного перехода резко возрастает по сравнению с нерезонансным положением этих уровней. Таким образом, процесс заселения различных колебательных состояний, зависящий от температуры, должен сильно сказываться на вероятности протекания туннельной реакции.
2. Величина и форма потенциального барьера на пути реакции принималась нами постоянной. В конденсированной фазе, однако, длина туннелирования определяется расстоянием между реагирующими частицами, которое все время изменяется за счет межмолекулярных колебаний. Рассмотрение процесса туннелирования через такой флуктуирующий барьер, который изменяет свою ширину и высоту, существенно меняет оценку вероятности туннелирования. а также предсказывает зависимость скорости процесса от температуры.
3. Рассматривая туннельный процесс, мы
предполагали, что координата туннельной реакции
совпадает с координатой надбарьерного перехода,
т.е. частица туннельным образом проделывает тот
же путь, что и при протекании надбарьерной
реакции. В реальности, конечно, туннельный
процесс может протекать по другому пути. Реакция
скорее всего пойдет по траектории, "срезающей
углы" или преодолевая узкие барьеры между
долинами исходных веществ и продуктов реакции.
Качественная иллюстрация таких траекторий
показана на Рис.5.11 для коллинеарной реакции AB + A ![]() A + AB для случая
mA >> mB.
A + AB для случая
mA >> mB.
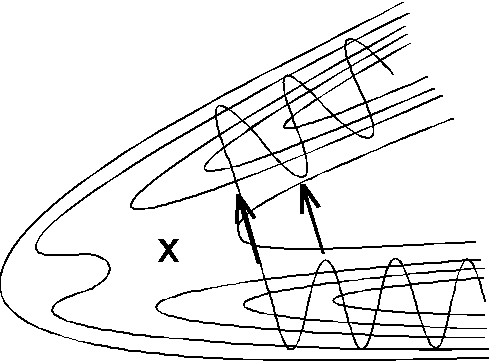
Туннельные траектории на рисунке не проходят через седловую точку, отмеченную крестиком, а преодолевают узкий потенциальный барьер между долинами исходных веществ и продуктов реакции. Реализация таких траекторий зависит не только от энергии, сконцентрированной на нормальной координате, отвечающей реакции, но и на других степенях свободы молекулы.
Представленная выше модель предлагает три критерия для определения того, протекает ли изучаемая экспериментально реакция по туннельному механизму.
1. Наличие туннельного расщепления энергетических уровней, которое может быть зафиксировано спектрально. Как уже отмечалось, этот критерий применим лишь к процессам, протекающим с большой частотой.
2. Наличие низкотемпературного предела скорости реакции. Этот критерий является достаточным, но не необходимым условием туннельного механизма реакции. Если для элементарной реакции наблюдается низкотемпературное плато, то можно говорить о доказательстве протекания этой реакции по туннельному механизму. Однако, если скорость реакции зависит от температуры, это еще не означает, что реакция протекает классическим путем. На протекание туннельной реакции указывает не только нулевая но и необычно маленькая экспериментально определенная энергия активации элементарной реакции.
3. Большой кинетический изотопный эффект, т.е. сильная зависимость скорости реакции от изотопного состава (массы) реагирующей частицы. Сильная зависимость от массы туннелирующего фрагмента предсказывается формулами (5.5) и (5.6). Они показывают, что туннелирующая масса входит в интеграл, находящийся в показателе степени экспоненты. В связи с этим представляется важным кратко проанализировать величины изотопных эффектов, которые следует ожидать при классическом и туннельном протекании реакции.
5.3 Кинетический изотопный эффект
Рассмотрим кратко возможные источники кинетического изотопного эффекта. Будем характеризовать изотопный эффект как отношение констант скорости одной и той же реакции, протекающей с исходными веществами разного изотопного состава. Поскольку максимальное изменение массы и других свойств при изотопном замещении достигается при замещении атомов водорода на атомы дейтерия, то подавляющее большинство теоретических и экспериментальных работ по кинетическому изотопному эффекту связано именно с этими изотопами.
В теории переходного состояния можно выделить три источника изотопных эффектов.
1. Изменение поступательной сумм по состояниям при изотопном замещении. Рассмотрим в качестве примера реакции:
CH4+ Cl ![]() CH3
+ HCl (5.11)
CH3
+ HCl (5.11)
CH3D + Cl ![]() CH3 +
DCl
CH3 +
DCl
Рассмотрение поступательных сумм по состояниям, которые, как мы помним, входят в предэкспоненциальный множитель в константе скорости реакции, предсказывает кинетический изотопный эффект, равный kH/kD = 1,065.
Приблизительно такие же небольшие эффекты получаются и для других реакций с участием тяжелых частиц, т.е. обыкновенных органических и неорганических молекул. Исключение составляют реакции с участием атомов водорода. Например, для реакций:
RH+ H. ![]() R. + H2
(5.12)
R. + H2
(5.12)
RH+ D. ![]() R. + HD
R. + HD
изотопный эффект за счет поступательных сумм по состояниям должен составлять kH/kD = 2,8.
2. Изменение колебательных сумм по состояниям при изотопном замещении.
Колебательные суммы по состояниям содержат множители
![]()
разлагая которые в ряд можно
приближенно оценить изотопный эффект 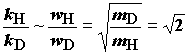
где w - частота нормального колебания с участием атома водорода, которое является координатой реакции.
3. Изменение высоты активационного барьера при изотопном замещении.
Вспомним, что высота активационного барьера,
которая проявляется в эксперименте как энергия
активации реакции, есть разница между энергией
нулевых колебаний исходного реакционного
комплекса и энергией нулевых колебаний
комплекса в области переходного состояния.
Энергия нулевых колебаний зависит от массы и
следовательно, частоты: ![]()
В высоту барьера, таким образом, входит величина
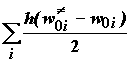
где суммирование ведется по всем колебательным степеням свободы. Большинство колебательных степеней свободы лишь незначительно изменяют частоту при переходе от исходных молекул к переходному состоянию и поэтому вносят незначительный вклад в энергию активации. Исключение составляет координата реакции, которая дает вклад в энергию активации, сравнимый с энергией нулевых колебаний. Таким образом, изменение энергии активации при замещении водорода на дейтерий может достигать величины:
![]()
т.е. почти треть энергии нулевых колебаний, что
составляет ~ 5,9 кДж/моль. Такая разница в энергиях
активации приведет при комнатной температуре к
изотопному эффекту kH/kD ![]() 10.
10.
Таким образом, экспериментальный изотопный эффект достигающий десяти, может объясняться в рамках надбарьерного перехода.
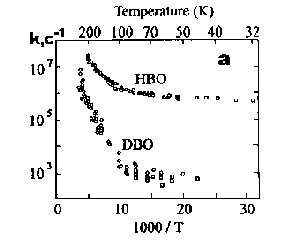
Для туннельных реакций изотопные эффекты могут изменяться в значительно большем диапазоне величин. На Рис.5.12а в координатах Аррениуса показаны температурные зависимости скорости туннельного переноса водорода и дейтерия в триплетном возбужденном состоянии производного бензоксазола (реакция Рис.5.9). Видно, что величина изотопного эффекта (Рис.5.12b) зависит от температуры и достигает величины 103.
 |
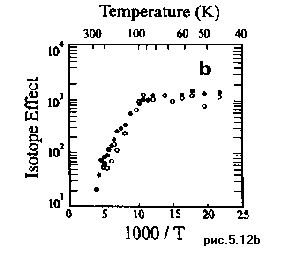 |
Максимальный изотопный эффект наблюдается в области низкотемпературного плато скорости реакции. В реакции, показанной на Рис.5.10, кинетический изотопный эффект изменяется от 40 до ~104 в температурном диапазоне 245 - 123К. В реакции (5.2) константа скорости реакции при дейтерировании уменьшается в 100-1000 раз. Таким образом, в реакциях туннелирования атома водорода кинетический изотопный эффект может составлять несколько порядков. В случае реакции, сопровождаемой туннелированием более тяжелых частиц, кинетический изотопный эффект, конечно, оказывается много меньше. Однако если на скорость надбарьерного протекания реакции изотопное замещение тяжелых атомов практически не влияет, то в туннельных реакциях изотопный эффект и в этом случае может быть экспериментально зафиксирован.
5.4 Задачи
1. Оцените критическую температуру туннелирования для реакции переноса атома водорода и атома дейтерия через барьер высотой 20 кДж/моль на расстояние 1Е .
2. Оцените критическую температуру туннелирования протона, если известно, что при комнатной температуре реакция протекает активационным образом с частотой 1010 с-1.
3. Оцените частоту туннелирования атома кислорода на расстояние 1Е и 0,1Е под барьером 40 кДж/моль.
4. Константа скорости присоединения мономерного звена в ходе туннельной полимеризации формальдегида при 4К составляет ~2х10-2 с-1. Оцените расстояние туннелирования, если считать,что туннелирует фрагмент CH2, а высота барьера состявляет 9,6 кДж/моль.
5. Оцените изотопный эффект для тунельной реакции переноса атома водорода на расстояние 0,5Е при высоте барьера 40 кДж/моль.
Литература.