Лекция 6. Спиновые и магнитные эффекты в химии
В ходе рассмотрения элементарного акта химической реакции мы оговаривали или негласно предполагали, что изучаемая реакция является разрешенной по спину. В реальности, однако, это условие выполняется не всегда. В этом разделе мы рассмотрим процессы, в ходе которых спиновые координаты оказывают влияние на протекание химической реакции.
Спиновое состояние молекулярных систем наиболее точно может быть описано с позиций квантовой механики. Такое теоретическое рассмотрение, однако, выходит за рамки настоящего курса. Поэтому в настоящем разделе будет дано лишь качественное описание спиновых и магнитных эффектов. Надо при этом иметь в виду, что качественные наглядные представления в квантовой механике неточны и часто вообще невозможны. Они могут использоваться лишь как упрощенная иллюстрация для и объяснение явлений, наблюдаемых в эксперименте. Для точного предсказания спиновых и магнитных эффектов в конкретных системах необходим точный квантово-механический анализ.
6.1 Спин микрочастицы
Собственный момент количества движения
микрочастицы, не связанный с ее перемещением как
целого, называется спином S. Спин
микрочастицы описывается спиновым квантовым
числом s. Абсолютное значение (по модулю) момента
количества движения микрочастицы составляет
величину ![]() S
S![]() =
= ![]() [s(s+1)]1/2
[s(s+1)]1/2
. Элементарные частицы, из которых состоят
молекулы - электрон, протон, нейтрон, имеют
спиновое квантовое число s = 1/2. Ядра и другие
микрообъекты, состоящие из нескольких
элементарных частиц, характеризуются целым или
полуцелым спиновым квантовым числом - 0, 1/2, 1, 3/2 и
т.п. Заряженные микрочастицы (электроны, протоны
и т. д.) имеют также магнитный момент ![]() , где g - гиромагнитное отношение,
, где g - гиромагнитное отношение, ![]() - магнетон Бора. Таким
образом, электроны, ядра, атомы и молекулы,
имеющие не равный нулю спин, представляют собой
микроскопические магниты.
- магнетон Бора. Таким
образом, электроны, ядра, атомы и молекулы,
имеющие не равный нулю спин, представляют собой
микроскопические магниты.
Проекция спинового момента количества
движения Sz на любую выбранную ось z в
пространстве квантована. Это означает, что
частица, имеющая спиновое квантовое число s,
может находиться в одном из (2s+1) состояний, в
которых ![]() , где ms
принимает от s до -s. Проекция магнитного момента
на ось z составляет
, где ms
принимает от s до -s. Проекция магнитного момента
на ось z составляет ![]() z
= -g
z
= -g ![]() ms.
Квантовые состояния с различными величинами
проекции момента количества движения и
магнитного момента на ось z являются
вырожденными по энергии (т.е. их энергия равна).
Вырождение снимается при наложении на систему
магнитного поля за счет взаимодействия
магнитного поля микрообъекта с внешним
магнитным полем (эффект Зеемана).
ms.
Квантовые состояния с различными величинами
проекции момента количества движения и
магнитного момента на ось z являются
вырожденными по энергии (т.е. их энергия равна).
Вырождение снимается при наложении на систему
магнитного поля за счет взаимодействия
магнитного поля микрообъекта с внешним
магнитным полем (эффект Зеемана).
Рассмотрим поведение частицы со спиновым квантовым числом а 1/2 во внешнем магнитном поле H.
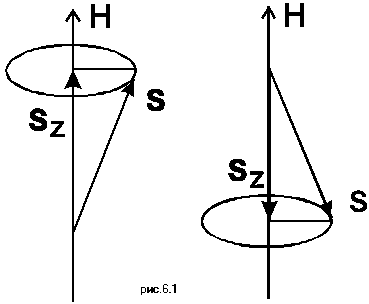
На Рис.6.1 видно, что в магнитном поле такая
частица находится в одном из двух зеемановских
состояний. В каждом из этих состояний внешнее
магнитное поле, взаимодействуя с собственным
магнитным моментом частицы, вызывает силу,
действующую на спин. В результате этого спин
прецессирует вокруг направления внешнего
магнитного поля. В одном состоянии проекция
магнитного момента спина направлена по
направлению внешнего поля, в другом состоянии -
против направления внешнего поля. Энергия этих
состояний отличается на величину ![]() E = g
E = g ![]() H.
H.
Если спиновое квантовое число системы превышает 1/2, то число возможных состояний больше. Для частицы с s=3/2 зависимость энергии четырех возможных спиновых состояний от напряженности магнитного поля показана на Рис.6.2.
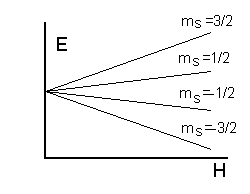
Таким образом, расщепление энергетического уровня системы во внешнем магнитном поле позволяет определить спиновое квантовое число системы. В дальнейшем абсолютное значение момента количества движения и магнитного момента микрочастиц нас интересовать не будет. Поэтому термин "спин" будет использоваться как краткое написание термина "спиновое квантовое число".
Объекты, энергетический уровень которых не расщепляется в магнитном поле, имеют спин, равный нулю. Говорят, что они находятся в синглетном спиновом состоянии. Если спин системы равен 1/2, система находится в дублетном состоянии, если спин равен 1 - в триплетном состоянии и т.д. Отметим, что для наглядности рассмотрение спиновых состояний мы будем производить, предполагая, что спины находятся во внешнем магнитном поле. Это предположение, однако, не ограничивает общности рассмотрения. Действительно, всегда можно учесть, что в радикальной паре каждый спин находится в магнитном поле партнера. Точнее, следует считать, что каждый спин находится в суммарном магнитном поле, в которое вносят вклад все магнитные частицы - электроны и ядра, находящиеся вблизи.
6.2 Реакции диссоциации и рекомбинации
Рассмотрим реакцию диссоциации молекулы по одной из ее связей. В ходе диссоциации двухатомной молекулы можно ожидать образования либо двух незаряженных атомов либо двух ионов - катиона и аниона
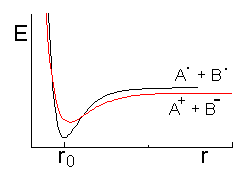 (Рис.6.3).
(Рис.6.3).
Если потенциальная энергия двух разделенных ионов меньше, чем потенциальная энергия двух разделенных атомов, наблюдается гетеролитическая диссоциация. В противоположном случае происходит гомолитический разрыв связи. Гетеролитическая диссоциация не представляет интереса с точки зрения спиновой динамики, поскольку такая реакция связана с перемещением пары электронов, суммарный спин которой равен нулю. В случае гомолитической диссоциации происходит разделение пары электронов, которые составляли химическую связь, и образование двух атомов или радикалов. Для двухатомной молекулы этот процесс можно проиллюстрировать диаграммой (Рис.6.4). На рисунке нижний по энергии терм соответствует паре электронов, находящихся на связывающей молекулярной орбитали и имеющих антипараллельные спины, т.е. суммарный спин системы в этом состоянии равен нулю (синглетное состояние). Диссоциативный терм представляет собой потенциальную энергию системы, в которой два электрона имеют параллельные спины. Суммарный спин системы при этом равен 1 (триплетное состояние). В соответствии с запретом Паули, эти электроны находятся на различных молекулярных орбиталях. Таким образом, триплетное состояние является электронно-возбужденным.
Так как незанятых молекулярных орбиталей в молекуле бесконечно много, каждая молекула имеет набор синглетных и набор триплетных возбужденных состояний. Некоторые возбужденные состояния могут быть чисто диссоциативными, или иметь небольшую энергию активации для процесса диссоциации. С учетом этого можно представить себе два различных механизма реакции диссоциации.
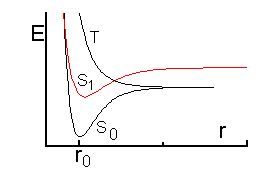 Рис.6.4
Рис.6.4
1. Термическая диссоциация из основного состояния. Для протекания такой диссоциации необходимая для разрыва связи энергия должна сконцентрироваться на соответствующей колебательной моде. Образующаяся пара радикалов имеет то же синглетное спиновое состояние, что и распавшаяся молекула, т.е. спины электронов антипараллельны.
2. Диссоциация из электронно-возбужденного состояния.
Электронно-возбужденные состояния молекулы обычно лежат достаточно высоко по энергии. Поэтому термическое возбуждение молекул в электронно-возбужденные состояния может происходить только при высоких температурах. Обычно электронно-возбужденные состояния получают, используя нетермические источники энергии, чаще всего свет. Заселение возбужденных состояний молекулы при поглощении фотона с последующей реакцией диссоциации называют реакцией фотодиссоциации. Поверхности потенциальной энергии молекулы в возбужденных электронных состояниях значительно отличаются по топологии от поверхности потенциальной энергии основного состояния. Это различие является причиной неожиданных химических превращений, которые изучает фотохимия. Для нас сейчас важно, что энергия активации реакции диссоциации в возбужденном синглетном состоянии может оказаться достаточно малой. В ходе такой реакции также образуется радикальная пара в синглетном спиновом состоянии. Молекула в возбужденном синглетном состоянии может претерпеть внутреннюю спиновую конверсию с переходом в триплетное состояние. Вероятность такого перехода зависит от разности энергий этих состояний, перекрывания их волновых функций, а также от величины спин-орбитального взаимодействия. Не рассматривая подробно эти зависимости, отметим лишь, что в некоторых молекулах заселение триплетного возбужденного состояния происходит с большой вероятностью, а в некоторых молекулах такой процесс практически запрещен. Триплетные возбужденные состояния также могут иметь небольшую энергию активации диссоциации. В случае реакции диссоциации из триплетного электронного состояния образуется пара радикалов с параллельными спинами, т.е. радикальная пара в триплетном состоянии.
Таким образом, в ходе реакции диссоциации, в зависимости от ее механизма, образуется пара радикалов или атомов либо в синглетном, либо в триплетном состоянии.
Рассмотрим теперь обратную реакцию рекомбинации двух радикалов. Если в такой реакции сталкивающиеся радикалы имеют антипараллельные спины (радикальная пара находится в синглетном суммарном состоянии), возможно образование химической связи. Такая реакция, как правило, протекает безактивационно, т.е. энергия активации реакции близка к нулю. Образующаяся молекула находится в основном электронном состоянии. Реакция протекает быстро и эффективно, если молекула имеет возможность отдать энергию, выделяющуюся при образовании связи, другим частицам или перераспределить ее между многими колебательными модами. Если сталкивающиеся радикалы имеют параллельные спины (радикальная пара находится в триплетном состоянии), то молекула может образоваться только в триплетном, возбужденном состоянии. Поскольку такие состояния обычно лежат высоко по энергии, в подавляющем большинстве случаев реакция рекомбинации в триплетной паре невозможна.
В качестве примера приведем реакцию фотодиссоциации перекиси бензоила (Рис.6.5).
В случае прямого фотолиза этого соединения образуется радикальная пара в синглетном состоянии. С помощью сенсибилизированного фотолиза ту же радикальную пару можно получить в триплетном состоянии. Синглетная радикальная пара с большей вероятностью рекомбинирует с образованием фенилбензоата. Триплетная радикальная пара с большей вероятностью выходит в объем растворителя, где вступает в другие реакции, в частности с молекулами растворителя RH. В эксперименте найдено, что для триплетных радикальных пар выход фенилбензоата составляет менее 3%, а для синглетных радикальных пар - более 10%
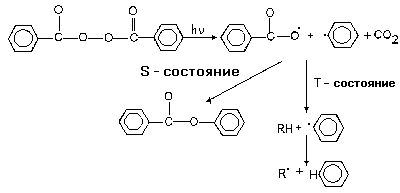
Рис.6.5
Рассмотрим теперь реакцию рекомбинации радикалов, которые зарождены по отдельности вдали друг от друга и реагируют при случайных столкновениях. В этом случае спиновое состояние пары сталкивающихся радикалов случайно. Радикальные пары, образующиеся в ходе случайных встреч, называются диффузионными радикальными парами. Часть таких пар находится в синглетном, а часть - в триплетном состоянии. Пусть рекомбинация радикалов происходит при наложенном на систему внешнем магнитном поле.
 |
||
 |
 |
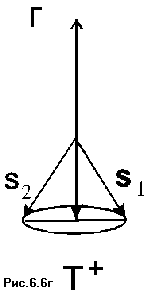 |
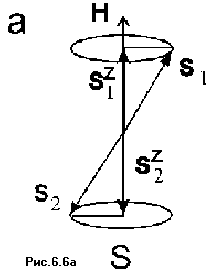
На Рис. 6.6(а) показаны радикалы, проекции магнитного момента которых оказались при встрече направленными в различные стороны, причем прецессия этих радикалов происходит в противофазе. В этом случае как суммарный спин системы двух радикалов, так и суммарная проекция их магнитных моментов оказывается равной нулю. Это означает, что радикальная пара находится в синглетном состоянии, в котором возможна реакция рекомбинации.
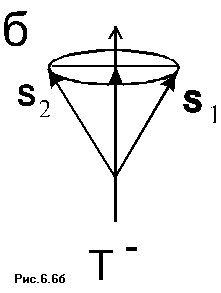
На Рис. 6.6 (б, в, г) суммарный спин пары равен единице. На Рис. 6.5(в) проекции магнитных моментов радикалов направлены в различные стороны и суммарная проекция равна нулю. Однако прецессия спинов происходит синфазно, и, таким образом, суммарный спин системы равен 1. На Рис. 6.6(б), проекции магнитных моментов обоих радикалов направлены по направлению внешнего магнитного поля, а на Рис. 6.6(г) - .против внешнего поля. Таким образом, при случайной встрече радикалов реализуется один из четырех вариантов спинового состояния пары - синглетное состояние S (s=0, m s=0) и три триплетных состояния T+, To, T-(s=1, ms = -1,0,1). В результате только 1/4 числа столкновений может привести к протеканию реакции рекомбинации, а 3/4 числа столкновений могут привести только к протеканию других конкурирующих реакций - реакциям с растворителем, с радикальными ловушками, изомеризации или диссоциации радикала и т.д..
Спиновые ограничения на возможность протекания реакции действуют не только в случае радикальных пар, но и при реакциях молекул со спином больше 1/2. В качестве примера приведем реакцию радикала с молекулой кислорода (Рис.6.7).
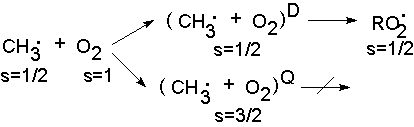
В этом случае реакция образования пероксидного радикала возможна, если реагенты встретились в дублетном состоянии (s=1/2) и запрещена, если они находятся в квартетном состоянии (s=3/2).
Приведенное рассмотрение показывает. что спиновое состояние реагирующих частиц в значительной степени определяет направление реакции и состав образующихся продуктов. Такое рассмотрение было бы исчерпывающим, если бы спиновое состояние реагирующих частиц не могло изменяться. Однако спиновое состояние пары реагентов подвижно. Поэтому для понимания вероятности протекания реакции по тому или иному направлению надо рассмотреть возможность изменения спинового состояния пары реагентов.
6.3 Молекулярная и спиновая динамика радикальных пар
Скорость изменения спинового состояния молекул и атомов принято характеризовать величинами T1 (время продольной релаксации или спин-решеточной релаксации) и T2 (время поперечной релаксации или спин-спиновой релаксации).
Проиллюстрируем эти характеристики следующим образом. Пусть в образце содержится ансамбль частиц со спином 1/2. Два состояния, в которых может находится каждая из этих частиц, показаны на Рис.6.1. В магнитном поле энергия этих состояний различна. Спины в образце заселяют эти два состояния в соответствии с распределением Максвелла-Больцмана. При этом разность равновесеых максвелл-больцмановских заселенностей двух состояний характеризует равновесную намагниченность образца, вызванную внешним магнитным полем. С помощью внешнего воздействия переведем часть спинов в другое состояние и, таким образом, изменим намагниченность образца. Например, спины с проекцией магнитного момента, расположенной по направлению внешнего поля превратим в спины с проекцией магнитного момента, направленной против направления магнитного поля. Нарушенное распределение начнет релаксировать к равновесию. Такая релаксация называется продольной, поскольку она приводит в равновесие наведенную намагниченность образца вдоль направления внешнего поля. Этот процесс происходит путем переворота спинов. Избыточная энергия при этом передается молекулам среды, окружающей спин.
Теперь представим себе, что весь ансамбль спинов, таких как на Рис.6.1, прецессирует в одной и той же фазе. Это означает, что образец выведен из равновесия, причем он имеет макроскопическую осциллирующую поперечную намагниченность. В ходе релаксации к равновесию спины, составляющие ансамбль, должны приобрести различную фазу прецессии, так чтобы суммарная поперечная намагниченность стала равной нулю. Это - процесс поперечной (спин-спиновой) релаксации. Времена магнитной релаксации Т1 и T2 органических и значительной части неорганических радикалов лежат в интервале 10-5 - 10-8 с.
Время столкновения двух молекул в газе не превышает времени одного колебания т.е. <10-13 c. Таким образом, за время столкновения молекул в газе спиновое состояние пары реагентов измениться не успевает. В связи с этим рассмотрение спиновых явлений в газофазных реакциях ограничивается вычислением вероятности столкновения в нужном спиновом состоянии, которое мы рассмотрели в предыдущем разделе.
Для конденсированной (жидкой и твердой) фазы характерен так называемый клеточный эффект. Это явление заключается в том, что сталкивающаяся пара молекул реагентов находится в клетке молекул растворителя, которые удерживают эту пару вместе значительное время
Рис 6.8.
В рамках теории Френкеля молекулы жидкости
почти все время находятся вблизи узлов
квазикристаллической решетки, совершая
колебания с частотой ~ 1013 c-1. Иногда
молекула жидкости перескакивает в соседний узел.
В жидкости с вязкостью ~ 1 сП время оседлой жизни
молекулы составляет ![]() 10-11 с. Это - оценка снизу времени жизни
радикальной пары относительно выхода радикалов
из клетки растворителя. Действительно, в
результате такого скачка пара радикалов
оказывается разделенной одним слоем молекул
растворителя, т.е. радикалы находятся во второй
координационной сфере друг друга. При случайных
скачках молекула из второй координационной
сферы с достаточно большой вероятностью снова
придет в соприкосновение со своим партнером.
Таким образом, действительное время жизни
радикальной пары несколько больше, чем время
оседлой жизни молекулы растворителя. Еще больше
это время становится, если учесть, что размеры
реагирующих частиц обычно больше, чем размеры
молекул растворителя, а частота скачков
соответственно меньше. Введем обобщенное
понятие клетки растворителя, как области
пространства, внутри которого вероятность
столкнуться для пары радикалов больше, чем
вероятность их реакции с посторонними
молекулами. Размер такой клетки для нейтральных
радикалов оказывается порядка 1 нм (10 Е ), а время
жизни в такой клетке порядка 10-9 с. Очевидно,
что время жизни пары относительно выхода из
клетки растет, если увеличивается вязкость
среды, достигая очень больших величин для
радикальных пар в твердой матрице. Время жизни
пары растет также в случае нахождения в клетке
противоположно заряженных частиц, например, пары
ион-радикалов, которые удерживаются в клетке
кулоновским взаимодействием. Таким образом, в
жидком растворителе у радикальной пары есть
время для спиновой эволюции, т.е. для перехода из
одного спинового состояния в другое. В обычных
условиях это время невелико, однако изменяя
условия эксперимента (вязкость и температуру),
его можно сделать сколь угодно большим.
10-11 с. Это - оценка снизу времени жизни
радикальной пары относительно выхода радикалов
из клетки растворителя. Действительно, в
результате такого скачка пара радикалов
оказывается разделенной одним слоем молекул
растворителя, т.е. радикалы находятся во второй
координационной сфере друг друга. При случайных
скачках молекула из второй координационной
сферы с достаточно большой вероятностью снова
придет в соприкосновение со своим партнером.
Таким образом, действительное время жизни
радикальной пары несколько больше, чем время
оседлой жизни молекулы растворителя. Еще больше
это время становится, если учесть, что размеры
реагирующих частиц обычно больше, чем размеры
молекул растворителя, а частота скачков
соответственно меньше. Введем обобщенное
понятие клетки растворителя, как области
пространства, внутри которого вероятность
столкнуться для пары радикалов больше, чем
вероятность их реакции с посторонними
молекулами. Размер такой клетки для нейтральных
радикалов оказывается порядка 1 нм (10 Е ), а время
жизни в такой клетке порядка 10-9 с. Очевидно,
что время жизни пары относительно выхода из
клетки растет, если увеличивается вязкость
среды, достигая очень больших величин для
радикальных пар в твердой матрице. Время жизни
пары растет также в случае нахождения в клетке
противоположно заряженных частиц, например, пары
ион-радикалов, которые удерживаются в клетке
кулоновским взаимодействием. Таким образом, в
жидком растворителе у радикальной пары есть
время для спиновой эволюции, т.е. для перехода из
одного спинового состояния в другое. В обычных
условиях это время невелико, однако изменяя
условия эксперимента (вязкость и температуру),
его можно сделать сколь угодно большим.
В качестве примера влияния спиновой эволюции на состав продуктов реакции рассмотрим реакцию бензилхлорида с бутиллитием:
| Ph-CH2Cl +LiC4H9 |
(Ph-CH2. + | .C4H9)S (6.1) |
A |
B |
Рекомбинация из синглетного состояния приведет к образованию продукта AB. Если за время жизни радикальной пары успеет пройти синглет-триплетная эволюция, то выход продукта внутриклеточной рекомбинации упадет. Триплетные пары радикалов с большой вероятностью распадутся, т.е. радикалы выйдут в объем растворителя. В ходе случайных блужданий они также рекомбинируют, но при этом образуется смесь продуктов AA, AB и BB.
Возможность протекания реакции и состав продуктов в примерах, приведенных в предыдущем разделе, также будет существенно меняться, если за время жизни пары реагентов в клетке растворителя будет протекать изменение спинового состояния системы. Поэтому рассмотрим скорость спиновой эволюции более подробно.
6.4 Скорость спиновой эволюции радикальных пар
Рассмотрим триплетную радикальную пару. Она
может находиться в одном из трех своих спиновых
состояний Т-, Тo и Т+. Как видно
из Рис.6.6, для перехода из Т- и Т+
состояний в синглетное состояние необходимо,
чтобы один из радикалов изменил направление
проекции магнитного момента на противоположное,
т.е. перевернулся. Этот процесс аналогичен
процессам, отвечающим за спин-решеточную
релаксацию. Для перехода из Тo в синглетное
состояние необходимо, чтобы синфазно
прецессирующие спины превратились в
прецессирующие в противофазе. Этот процесс,
связанный с изменением фазы прецессирующего
спина, аналогичен процессу спин-спиновой
релаксации. Вообще говоря, для определения
скорости триплет-синглетной эволюции необходимо
учитывать вероятность всех трех переходов: Т-![]() S, Тo
S, Тo![]() S и Т+
S и Т+![]() S. Однако, наибольший
вклад будет давать переход, при котором энергия
системы изменяется меньше всего. В магнитном
поле энергия Т- и Т+ состояний
пропорциональна напряженности магнитного поля,
а энергия состояний S и То не зависит от
напряженности поля. Качественно энергетическое
расположение уровней в сильном магнитном поле
показано на Рис.6.9.
S. Однако, наибольший
вклад будет давать переход, при котором энергия
системы изменяется меньше всего. В магнитном
поле энергия Т- и Т+ состояний
пропорциональна напряженности магнитного поля,
а энергия состояний S и То не зависит от
напряженности поля. Качественно энергетическое
расположение уровней в сильном магнитном поле
показано на Рис.6.9.
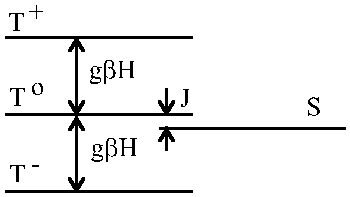
Таким образом, наибольший вклад в процесс триплет-синглетной эволюции вносит процесс перехода из То состояния, энергия которого отличается от энергии синглетного состояния на величину энергии обменного взаимодействия J.
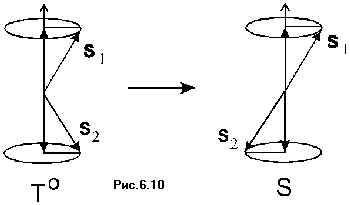
Из Рис.6.10 видно, что для осуществления T ![]() S перехода разность фаз
между прецессирующими спинами должна достигнуть
величины
S перехода разность фаз
между прецессирующими спинами должна достигнуть
величины ![]() . Такая
разность фаз может накопиться, только если два
спина будут прецессировать с ра
. Такая
разность фаз может накопиться, только если два
спина будут прецессировать с ра
зличными частотами. Частота прецессии каждого спина соответствует частоте соответствующего ЭПР перехода. Таким образом, она может быть записана в виде:
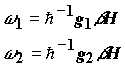 (6.2)
(6.2)
где ![]() 1 и
1 и ![]() 2 - частоты
прецессии первого и второго спинов,
2 - частоты
прецессии первого и второго спинов, ![]() - магнетон Бора, g1 и
g2-g-факторы двух радикалов.
- магнетон Бора, g1 и
g2-g-факторы двух радикалов.
Отсюда время триплет-синглетной эволюции:
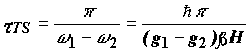 (6.3)
(6.3)
Таким образом, скорость триплетного перехода
тем больше, чем больше разность g-факторов
радикалов в радикальной паре. Такой механизм
спиновой эволюции называется ![]() g-механизмом. Из приведенной формулы
также видно, что скорость спиновой эволюции
зависит от напряженности магнитного поля. С
учетом возможности спиновой конверсии всех трех
триплетных спиновых состояний эта зависимость
имеет более сложный характер, чем это
предполагает формула (6.3). Однако, даже не
углубляясь в более подробное рассмотрение этой
зависимости, можно сказать, что магнитное поле
способно изменить направление химических
превращений, которые определяются спиновым
состоянием реагентов. Это качественное
рассмотрение объясняет, каким образом магнитные
воздействия, энергия которых много меньше
энергии теплового движения и, тем более, меньше
энергетических характеристик химических связей,
тем не менее способно влиять на химические
реакции.
g-механизмом. Из приведенной формулы
также видно, что скорость спиновой эволюции
зависит от напряженности магнитного поля. С
учетом возможности спиновой конверсии всех трех
триплетных спиновых состояний эта зависимость
имеет более сложный характер, чем это
предполагает формула (6.3). Однако, даже не
углубляясь в более подробное рассмотрение этой
зависимости, можно сказать, что магнитное поле
способно изменить направление химических
превращений, которые определяются спиновым
состоянием реагентов. Это качественное
рассмотрение объясняет, каким образом магнитные
воздействия, энергия которых много меньше
энергии теплового движения и, тем более, меньше
энергетических характеристик химических связей,
тем не менее способно влиять на химические
реакции.
Кроме ![]() g-механизма
известен еще один не менее важный механизм,
приводящий к изменению скорости прецессии
спинов. Это механизм сверхтонкого
взаимодействия (СТВ-механизм). Этот механизм
может играть роль, если радикалы в радикальной
паре имеют в своей структуре магнитные ядра.
Действительно, магнитное ядро создает
дополнительное магнитное поле на неспаренном
электроне. Энергия электронного спина или, что то
же, частота его прецессии меняется вследствие
наложения этого дополнительного поля. Пусть один
из радикалов пары имеет в своей структуре протон
- магнитное ядро с ядерным спином 1/2. При обычных
температурах у половины таких радикалов
проекция магнитного момента ядра направлена по
направлению внешнего магнитного поля, а у
половины радикалов - против этого направления.
Частота прецессии для этих радикалов будет
составлять:
g-механизма
известен еще один не менее важный механизм,
приводящий к изменению скорости прецессии
спинов. Это механизм сверхтонкого
взаимодействия (СТВ-механизм). Этот механизм
может играть роль, если радикалы в радикальной
паре имеют в своей структуре магнитные ядра.
Действительно, магнитное ядро создает
дополнительное магнитное поле на неспаренном
электроне. Энергия электронного спина или, что то
же, частота его прецессии меняется вследствие
наложения этого дополнительного поля. Пусть один
из радикалов пары имеет в своей структуре протон
- магнитное ядро с ядерным спином 1/2. При обычных
температурах у половины таких радикалов
проекция магнитного момента ядра направлена по
направлению внешнего магнитного поля, а у
половины радикалов - против этого направления.
Частота прецессии для этих радикалов будет
составлять:
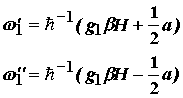 (6.4)
(6.4)
где ![]() - энергия
сверхтонкого взаимодействия.
- энергия
сверхтонкого взаимодействия.
Разность частот прецессии, которая приводит к спиновой конверсии, составит:
![]() (6.5)
(6.5)
Таким образом, в такой радикальной паре
скорость спиновой конверсии определяется
одновременно ![]() g- и
СТВ- механизмами. Видно, что она зависит от
направления ядерного спина в магнитном поле
(знаки '+' и '-' в формуле 6.5).
g- и
СТВ- механизмами. Видно, что она зависит от
направления ядерного спина в магнитном поле
(знаки '+' и '-' в формуле 6.5).
Из формулы (6.5) следуют два наиболее ярких спиновых эффекта в химии - магнитный изотопный эффект и эффект спиновой поляризации ядер.
6.5 Магнитный изотопный эффект
Из формулы (6.5) видно, что наличие магнитного ядра влияет на скорость синглет-триплетной эволюции радикальной пары, и, таким образом, на направление химического превращения. Рассмотрим химическое соединение, состоящее из смеси молекул различного изотопного состава. Часть молекул содержит ядра с неравным нулю спином, а часть молекул состоит из немагнитных ядер. В результате сверхтонкого взаимодействия скорость триплет-синглетной эволюции молекул, содержащих магнитные ядра, и немагнитных молекул будет различной.
В качестве примера рассмотрим реакцию фотодиссоциации дибензилкетона из триплетного возбужденного состояния (Рис.6.11). В ходе такой диссоциации первоначально образуется триплетная радикальная пара. В этой радикальной паре соединенный с кислородом атом углерода может оказаться немагнитным (изотоп 12С, s=0) или магнитным (изотоп 13С, s=1/2). Радикальные пары, имеющие немагнитный изотоп углерода, довольно долго находятся в триплетном состоянии. За это время успевает пройти реакция декарбонилирования ацильного радикала. В результате рекомбинации получается молекула дибензила. Радикальные пары, имеющие магнитный изотоп углерода, быстро переходят из триплетного в синглетное спиновое состояние, в котором протекает рекомбинация с образованием исходного дибензилкетона. Таким образом, в ходе этой реакции в исходном веществе будут накапливаться молекулы, содержащие изотоп 13C в карбонильной группе. Образующаяся оксид углерода содержит в большей степени изотоп 12С. Явление обогащения и обеднения различных продуктов реакции магнитными изотопами носит название магнитного изотопного эффекта.
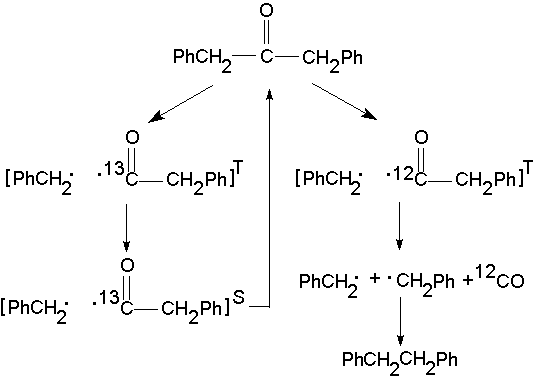
Рис.6.11.
Пусть содержание магнитного изотопа в исходном
соединении ![]() о ,
а текущее содержание этого изотопа в продукте
реакции
о ,
а текущее содержание этого изотопа в продукте
реакции ![]() . Тогда
степень изотопного обогащения этого продукта S=
. Тогда
степень изотопного обогащения этого продукта S=![]() /
/![]() о.
о.
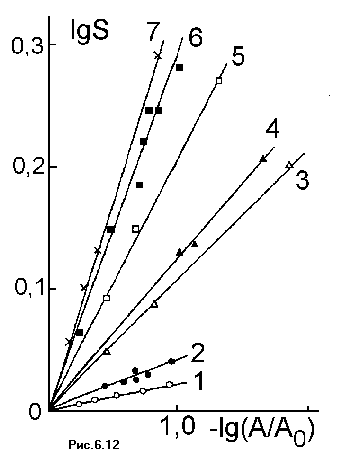
На Рис. 6.12 показана экспериментальная зависимость степени обогащения исходного соединения изотопом 13С от степени превращения, измеренная в различных растворителях (1- бензол; 2- гексан; 3- циклогексанол 20оС; 4-. циклогексанол 0оС; 5- глицерин, 1700сПз; 6- мицеллы гексадецилтриаммоний хлорида в воде; 7- гицерин, 2400 сПз).
Видно, что в различных растворителях разделение изотопов происходит с различной эффективностью. Наибольшее разделение достигается в вязких растворителях. Это не удивительно, поскольку спиновая эволюция требует времени. Вклад спиновых эффектов может иметь место только в тех условиях, когда время жизни радикальной пары сравнимо с характеристическим временем спиновой эволюции. Такие условия реализуются в вязких растворителях.
Экспериментально найдены реакции, в ходе которых магнитный изотопный эффект наблюдается на следующих парах изотопов: 12С/13С, 16O/17O/18O, 32S/33S/34S, 28Si/29Si/30Si, 238U/235U.
6.6 Эффект химической поляризации ядер и электронов (ХПЯ и ХПЭ)
Под спиновой поляризацией ядер и электронов понимают разность заселенностей спиновых состояний соответственно ядер или электронов, находящихся в магнитном поле (разность заселенностей зеемановских уровней). В состоянии равновесия эта разность заселенностей описывается максвелл-больцмановским распределением.
Различными воздействиями на систему можно достигнуть неравновесной заселенности зеемановских уровней, т.е. неравновесной поляризации. Химической поляризацией ядер называется эффект возникновение неравновесной заселенности ядерных зеемановских уровней в результате протекания химической реакции. Очевидно, что неравновесная поляризация может быть зарегистрирована, только если время измерения заселенностей меньше, чем время установления равновесного распределения, т.е. меньше, чем время ядерной магнитной релаксации. Время магнитной релаксации ядер довольно велико. Оно обычно лежит в интервале от 0,1 до 10 с. (Как мы уже говорили, время магнитной релаксации электронных спинов лежат в интервале 10-5 - 10-8 с).
Существует только один широко распространенный метод измерения заселенностей ядерных и электронных зеемановских уровней - метод магнитного резонанса.
Напомним, что для наблюдения магнитного резонанса образец помещают в постоянное магнитное поле. Энергия различных спиновых состояний зависит от напряженности магнитного поля, как это показано на Рис.6.13.
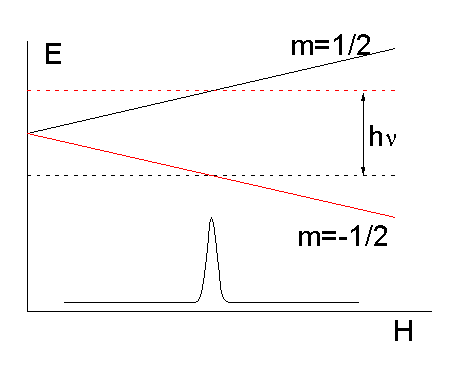
Рис.6.13
На образец направляется электромагнитное излучение и регистрируется его поглощение. Если энергия кванта электромагнитного поля соответствует разности энергии зеемановских уровней, наблюдается пик резонансного поглощения. Амплитуда этого пика пропорциональна разности заселенностей зеемановских уровней.
Рассмотрим реакцию, содержащую радикальную стадию (Рис.6.14). На рисунке X - немагнитный заместитель.
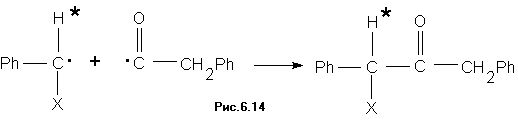
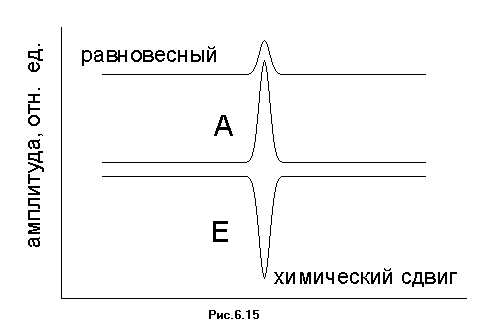
В спектре ЯМР продукта этой реакции, когда он находится в равновесии, можно выделить пик поглощения, соответствующий переходу между зеемановскими уровнями протона, который отмечен на схеме звездочкой. Этот пик показан на Рис.6.15.
Теперь будем регистрировать спектр ЯМР этого
же продукта непосредственно в ходе химической
реакции его образования. Пусть радикальная пара,
в ходе рекомбинации которой он образуется,
исходно получается в триплетном состоянии.
Разность частот прецессии в радикальной паре
описывается выражениям (6.5). Она различна для пар,
ядерный спин протона в которых ориентирован по и
против внешнего магнитного поля. Это различие
заключается в знаке перед членом описывающим
сверхтонкое взаимодействие в (6.5). Пусть величина ![]() g отрицательна. Тогда
скорость триплет-синглетной конверсии
радикальных пар, которые содержат протон со
спином, направленным по полю, окажется меньше,
чем скорость конверсии пар со спином протона,
направленным против поля. Это означает, что
последние пары будут быстрее претерпевать
спиновую эволюцию в синглетное состояние и,
следовательно, рекомбинировать с образованием
продукта реакции. В результате в продукте
реакции окажется больше молекул, ядерный спин
которых направлен против направления внешнего
магнитного поля. Эта ситуация является
неравновесной, поскольку зеемановский уровень с
большей энергией заселен больше, чем
зеемановский уровень с меньшей энергией. В
результате, вместо поглощения в условиях
резонанса будет происходить испускание
электромагнитных волн с резонансной частотой. На
спектре ЯМР резонансный пик изменяет знак, как
это показано на Рис.6.15. Такой пик обозначают
буквой E (emission).
g отрицательна. Тогда
скорость триплет-синглетной конверсии
радикальных пар, которые содержат протон со
спином, направленным по полю, окажется меньше,
чем скорость конверсии пар со спином протона,
направленным против поля. Это означает, что
последние пары будут быстрее претерпевать
спиновую эволюцию в синглетное состояние и,
следовательно, рекомбинировать с образованием
продукта реакции. В результате в продукте
реакции окажется больше молекул, ядерный спин
которых направлен против направления внешнего
магнитного поля. Эта ситуация является
неравновесной, поскольку зеемановский уровень с
большей энергией заселен больше, чем
зеемановский уровень с меньшей энергией. В
результате, вместо поглощения в условиях
резонанса будет происходить испускание
электромагнитных волн с резонансной частотой. На
спектре ЯМР резонансный пик изменяет знак, как
это показано на Рис.6.15. Такой пик обозначают
буквой E (emission).
При других магнитных параметрах возможна обратная ситуация, когда неравновесность заключается в избыточной заселенности нижнего по энергии зеемановского уровня. В этом случае в спектре ЯМР будет наблюдаться пик поглощения, но его амплитуда может многократно превышать обычную. Такие пики обозначают буквой A (absorption). Если радикал в радикальной паре имеет в своей структуре несколько групп эквивалентных протонов, в спектре ЯМР наблюдается мультиплетное расщепление. Часто в таких мультиплетах часть пиков демонстрирует эмиссию, а часть аномальное поглощение. Мультиплетный эффект ХПЯ можно также легко объяснить на основе рассмотрения скорости спиновой эволюции пары с учетом сверхтонкого взаимодействия со всеми протонами.
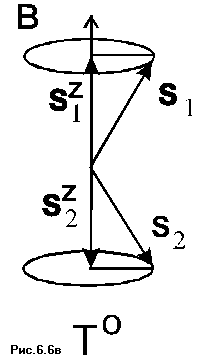
Эффект химической поляризации электронов, т.е. возникающей в ходе реакции неравновесной заселенности электронных зеемановских уровней, экспериментально зафиксировать значительно сложнее. Это связано с тем, что время релаксации спинов электронов (установления равновесной заселенности) значительно меньше. Качественно возможность явления ХПЭ проиллюстрируем следующим образом. Пусть изучается реакция диссоциации молекулы из триплетного возбужденного состояния. Во внешнем магнитном поле три спиновых состояния триплетной молекулы имеют различную энергию
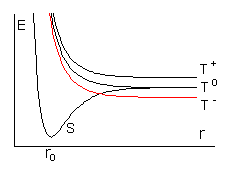
Рис.6.16.
Переход из триплетного в синглетное состояние, необходимый для протекания обратной реакции рекомбинации, быстрее всего происходит при равенстве нулю энергий состояний, т.е. при пересечении уровней энергии. Из Рис. 6.16 видно, что Т- и Тo термы пересекаются с S термом, а терм Т+ не пересекается. Таким образом, молекулы в первых двух состояниях с большей вероятностью перейдут в синглетное состояние, в котором легко рекомбинируют с образованием исходной молекулы. В продукте реакции диссоциации будет значительная часть частиц, образовавшихся при диссоциации Т+ возбужденного состояния исходной молекулы. Это означает, что образовавшиеся при диссоциации радикалы находятся на верхнем по энергии зеемановском уровне. Такие радикалы должны давать эмиссионный резонансный пик в спектре ЭПР.
6.7 Вторая генерация магнитных эффектов
Мы показали причины, объясняющие наблюдение
магнитных эффектов трех типов - влияние
магнитного поля на химическое превращение,
магнитный изотопный эффект и ХПЯ (ХПЭ). В этих
процессах эволюция спиновых состояний, которая
определяет суть явления, происходит спонтанно,
под действием естественных условий в изучаемой
системе. Между тем, с помощью воздействия
микроволновым электромагнитным излучением
можно оказывать контролируемое влиянияние на
спиновую эволюцию системы. Действительно,
рассмотрим триплетную радикальную пару в
магнитном поле. Вследствие близости
энергетических уровней в естественных условиях
быстрее всего происходит Тo![]() S конверсия. Однако микроволновое облучение
искусственно вызывает Т+
S конверсия. Однако микроволновое облучение
искусственно вызывает Т+![]() Тo
и Т-
Тo
и Т-![]() Тo переходы. Таким образом,
если облучение с достаточной мощностью
происходит в условиях резонанса между этими
уровнями, все триплетные молекулы с одинаковой
вероятностью способны перейти в синглетное
состояние и вступить в реакцию
Тo переходы. Таким образом,
если облучение с достаточной мощностью
происходит в условиях резонанса между этими
уровнями, все триплетные молекулы с одинаковой
вероятностью способны перейти в синглетное
состояние и вступить в реакцию
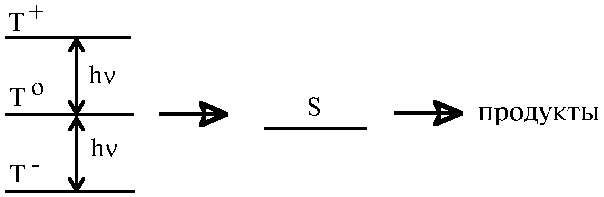
Рис.6.17.
В этих условиях скорость реакции растет. На этом принципе основан метод детектирования магнитного резонанса по выходу химической реакции - RYDMR (reaction yield detection of magnetic resonance). Вариантом этого метода является оптически детектируемый магнитный резонанс (ODMR), который основан на регистрации выхода реакции по люминесценции продуктов реакции. Чувствительность оптической регистрации, которая способна фиксировать отдельные фотоны света, приводит к тому, что этим методом иногда можно зафиксировать спектр ЭПР частиц, общее число которых в образце всего 103-105 (при обычной чувствительности метода ЭПР 1011-1013 частиц в образце).
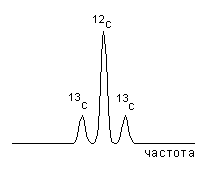
Рассмотрим снова триплетные радикальные пары, в которые входят радикалы с различным изотопным составом. На Рис.6.18 показан спектр ЭПР одного из радикалов пары, центральный пик которого соответствует частицам, содержащим изотоп 12C, а боковые компоненты - радикалам с изотопом 13C. Если микроволновое облучение будет иметь резонансную частоту центрального пика, то для пар, содержащих эти радикалы увеличится скорость триплет-синглетной конверсии. В результате увеличится выход продукта реакции, содержащего изотоп 12C. Облучение в сателлитные линии поглощения увеличит выход продуктов реакции с изотопом 13C.
Таким образом, экспериментатор в состоянии искусственно вызывать изотопный эффект. Это явление получило название стимулированного изотопного эффекта (SIE).
Теперь предположим, что микроволновое облучение производится в боковую компоненту этого спектра, соответствующую направлению магнитного момента ядра 13С против поля. В таком случае, в продукте реакции увеличится число молекул с таким же образом направленными спинами ядер. В спектре ЯМР будет наблюдаться стимулированная поляризация ядер (эффект SNP - stimulated nuclear polarization).
Таким образом, ко второму поколению магнитных эффектов относятся явления, связанные с воздействием на химическую реакцию резонансного микроволнового облучения.
6.8 Задания
1. Оцените степень равновесной поляризации протонов в ЯМР-спектрометре (200 МГц) при 300К, 77К, 4К.
2. Оцените степень равновесной спиновой поляризации в ЭПР-спектрометре (3 см) при 300К, 77К, 4К.
3. Оцените время синглет-триплетной эволюции в
поле 3000 Гс радикальной пары, одним из радикалов
которой является атом водорода, а другой не имеет
магнитных ядер. Константа СТВ на протоне 500Гс, ![]() g=0,001.
g=0,001.
4. Оцените время синглет-триплетной эволюции в
поле 3000 Гс радикальной пары, одним из радикалов
которой является СН3, а другой не имеет магнитных
ядер. Константа СТВ на протоне 23 Гс, ![]() g = 0,01.
g = 0,01.
5. Оцените долю геминальной (внутриклеточной) рекомбинации исходно триплетной радикальной пары при следующих условиях:
время жизни пары 10-9 с, время синглет-триплетной релаксации 10-8 с.
6. Оцените величину магнитного изотопного эффекта при рекомбинации исходно триплетной радикальной пары при следующих условиях:
магнитное поле 3000 Гс, время жизни пары 10-9с,
![]() g = 0,001, константа
СТВ на изотопе 13С а = 10 Гс.
g = 0,001, константа
СТВ на изотопе 13С а = 10 Гс.
7. Оцените максимальную ядерную поляризацию
(ХПЯ) которая может быть зафиксирована в спектре
ЯМР (200 МГц) в продуктах рекомбинации триплетной
радикальной пары, содержащей один протон, ![]() g = 0,001, константа СТВ
на протоне 20 Гс, время жизни пары 10-9с.
g = 0,001, константа СТВ
на протоне 20 Гс, время жизни пары 10-9с.
Литература.